9. Heaps

The word heap is used in a couple of different contexts in Computer Science. A heap sometimes refers to an area of memory used for dynamic (i.e. run-time) memory allocation. Another meaning, and the topic of this chapter, is a data structure that is conceptually a complete binary tree. Heaps are used in implementing priority queues, the heapsort algorithm, and some graph algorithms. Heaps are somewhat like binary search trees in that they maintain an ordering of the items within the tree. However, a heap does not maintain a complete ordering of its items. This has some implications for how a heap may be used.

9.1. Heap Program

Here you can download a starter shell for the heap implementation described in the chapter. To run this program you must also download the person.py file. Place both modules in the same directory. The heap.py program file contains a main function to test your heap implementation.

This heap program can be modified to support a different number of children. For instance, a four child heap is also possible. The file defaults to a three child heap.

'''
  File:  heap.py
  Author: 
  Date:
  Description:  This module provides the class Heap.  We can create heaps which
     are either largest-on-top or smallest-on-top.  We can also create heaps 
     with a maximum number of children of our choice.  As written, the default
     number of children is 3 and the default initial capacity is 5.  These
     parameters can be changed by the way we invoke the class constructor.
     
     The module also provides the efficient heap sort method.  By default, the
     methods sorts objects in increasing order.  But we can also sort objects
     in decreasing order.
     
     Our implementation works for objects of any class that understand the
     relational operators.

'''

testing = False
from person import Person
import math

def heapSort(aSequence, increasingOrder = True):
  '''  This method will answer a list of the elements of aSequence, which
   by default will be sorted in increasing order.  To sort in decreasing
   order, send a second parameter which is False.
  '''
  # Do last, after buildFrom() and siftDownFrom(), other methods.
  # More code needed!
  return h.data[:]


class Heap:
  '''
  The class Heap provides a generic heap abstract data type.
  The instances of this class can hold objects of any sort that
  understand the relational operators.  It also allows us to create
  heaps with any maximum number of children.
  '''

  DefaultCapacity = 5           #  A class variable
  DefaultNumberOfChildren = 3   #  Another class variable

  def __init__(self, capacity = DefaultCapacity,
          largestOnTop = True, numberOfChildren =
              DefaultNumberOfChildren):
    self.size = 0
    self.capacity = capacity
    self.largestOnTop = largestOnTop
    self.data = [None]*capacity
    self.maxChildren = numberOfChildren

  def __str__(self):
    if self.largestOnTop:
       sortOfHeap = 'largest on top'
    else:
       sortOfHeap = 'smallest on top'
    st = 'It is a ' + sortOfHeap + ' heap:\n'
    #  .......
    return st

  def addToHeap(self,newObject):
    '''If the heap is full, double its current capacity.
       Add the newObject to the heap, maintaining it as a
       heap of the same type.  Answer newObject.
    '''
    pass  # Allows compilation of file.  Replace with actual code.

  def bestChildOf(self, index, lastIndex):
    ''' Answer the index of the "best child" of self.data[index], if it
      exists. If not, answer None.  lastIndex is the index of the last 
      object in the heap.  For a largest on top heap, the best child is the
      largest child.  For a smallest on top heap, it is the smallest child
      of the node with the given index.
    '''
    bestChild = None
    #  .......
    return bestChild
            
  def buildFrom(self, aSequence):
    '''aSequence is an instance of a sequence collection which
        understands the comparison operators. The elements of
        aSequence are copied into the heap and ordered to build
        a heap. '''
    pass

  def removeTop(self):
    '''  If the heap is not empty, remove the top element
      of the heap and adjust the heap accordingly.  Answer the object
      removed.  If the heap is empty, return None.
    '''
    pass

  def siftDownFrom( self, fromIndex ):
    '''fromIndex is the index of an element in the heap.
      Pre: data[fromIndex..size-1] satisfies the heap condition,
      except perhaps for the element self.data[fromIndex].
      Post:  That element is sifted down as far as neccessary to
      maintain the heap structure for data[fromIndex..size-1].
    '''
    pass

  def __siftUpFrom(self, child):
    ''' child is the index of a node in the heap.  This method sifts
      that node up as far as necessary to ensure that the path to the root
      satisfies the heap condition. '''
    pass

  def __siftDownFromTo(self, fromIndex, lastIndex):
    '''fromIndex is the index of an element in the heap.
      Pre: data[fromIndex..lastIndex] satisfies the heap condition,
      except perhaps for the element data[fromIndex].
      Post:  That element is sifted down as far as neccessary to
      maintain the heap structure for data[fromIndex..lastIndex].'''
    pass
    
  def levelByLevelString(self):
    ''' Return a string which lists the contents of the heap
       level by level.
    '''
    index = 0 # start at the root node
    maxLevel = \
       math.ceil(math.log(self.size*(self.numberOfChildren - 1) + 1)/
            math.log(self.numberOfChildren))
    #  MORE!              

  #  Other methods?
  #  Use Doc strings for all methods!
        
def main():
  print("My name is ")
  h = Heap()
  h.addToHeap(20)
  h.addToHeap(40)
  h.addToHeap(-10)
  h.addToHeap(72)
  h.addToHeap(84)
  h.addToHeap(-100)
  h.addToHeap(54)
  h.addToHeap(66)
  h.addToHeap(99)
  h.addToHeap(1000)
  h.addToHeap(900)
  print(h)

  h.data[0] = 50
  h.siftDownFrom(0)
  print(h)

  h.data[0] = 60
  h.siftDownFrom(0)
  print(h)

  h = Heap(3, False)
  h.buildFrom((20,40,-10, 72, 84, -100, 54,66, 99))
  print(h)

  theList = heapSort([10, 30, -100, 50, 20, 30, -40,70, 5, 50])
  print(theList)

  theList = heapSort([10, 30, -100, 50, 20, 30, -40,70, 5, 50], False)
  print(theList)

  print( "\nThe following is the extra output that happens when we" )
  print( " create a heap that can have 5 children per node. \n" )
  heap = Heap(numberOfChildren = 5)
  heap.buildFrom((10, 20, -29, 16, 70, 30, 20, 100, 38, -293, \
   77, -19, -77, 230, 91, -230, -48, 23))
  print(heap)

  a = heapSort((10, 20, -29, 16, 70, 30, 20, 100, 38, -293, \
   77, -19, -77, 230, 91, -230, -48, 23))
  print(a)


  #  Extra stuff to test removeTop()
  h = Heap()
  h.addToHeap(20)
  h.addToHeap(40)
  h.addToHeap(-10)
  h.addToHeap(72)
  h.addToHeap(84)
  h.addToHeap(-100)
  h.addToHeap(54)
  h.addToHeap(66)
  h.addToHeap(99)
  h.addToHeap(1000)
  h.addToHeap(900)
  print(h)

  print(h.removeTop())
  print(h)

  print( "trying heapSort method:" )
  print( heapSort((20, -30, 45, 921, 37, 200, -1000, 4000, 57)) )
  print(  heapSort((20, -30, 45, 921, 37, 200, -1000, 4000, 57), False))
  joe = Person('Joe', 99)
  jill = Person('Jill', 200)
  walt = Person('Walter', 3000)
  dave = Person('David', 23)
  kent = Person('Kent', 220)
  alan = Person('Al', 110)
  folks = [joe, jill, walt, dave, kent, alan]
  print( heapSort(folks) )
  print( heapSort(folks, False ))

  h = Heap()
  h.addToHeap(20)
  h.addToHeap(40)
  h.addToHeap(-10)
  h.addToHeap(72)
  h.addToHeap(84)
  h.addToHeap(-100)
  h.addToHeap(54)
  h.addToHeap(66)
  h.addToHeap(99)
  h.addToHeap(1000)
  h.addToHeap(900)
  print()
  print( 'A level by level listing of the heap:' )
  print( h.levelByLevelString() )


if __name__ == '__main__': main()

'''  The following is the output from running this code:
My name is YOUR NAME
[evaluate heap.py]
It is a largest on top heap:
The size of the heap is 11.
The capacity of the heap is 20.
The elements of the heap are: 
1000
72
99
900
20
-100
54
-10
66
84
40

It is a largest on top heap:
The size of the heap is 11.
The capacity of the heap is 20.
The elements of the heap are: 
900
72
99
50
20
-100
54
-10
66
84
40

It is a largest on top heap:
The size of the heap is 11.
The capacity of the heap is 20.
The elements of the heap are: 
99
72
84
50
20
-100
54
-10
66
60
40

Output from buildFrom():
It is a smallest on top heap:
The size of the heap is 9.
The capacity of the heap is 9.
The elements of the heap are: 
-100
20
-10
72
84
40
54
66
99

[-100, -40, 5, 10, 20, 30, 30, 50, 50, 70]
[70, 50, 50, 30, 30, 20, 10, 5, -40, -100]

The following is the extra output that happens when we
 create a heap that can have 5 children per node. 

It is a largest on top heap:
The size of the heap is 18.
The capacity of the heap is 18.
The elements of the heap are: 
230
100
91
23
70
30
20
20
38
-293
77
-19
-77
-29
10
-230
-48
16

[-293, -230, -77, -48, -29, -19, 10, 16, 20, 20, 23, 30, 38, 70, 77, 91, 100, 230]
It is a largest on top heap:
The size of the heap is 11.
The capacity of the heap is 20.
The elements of the heap are: 
1000
72
99
900
20
-100
54
-10
66
84
40

Output from removeTop():
1000
It is a largest on top heap:
The size of the heap is 10.
The capacity of the heap is 20.
The elements of the heap are: 
900
72
99
40
20
-100
54
-10
66
84

trying heapSort method:
[-1000, -30, 20, 37, 45, 57, 200, 921, 4000]
[4000, 921, 200, 57, 45, 37, 20, -30, -1000]
[Name: David Id: 23 , Name: Joe Id: 99 , Name: Al Id: 110 ,
   Name: Jill Id: 200 , Name: Kent Id: 220 , Name: Walter Id: 3000 ]
[Name: Walter Id: 3000 , Name: Kent Id: 220 , Name: Jill Id: 200 , 
   Name: Al Id: 110 , Name: Joe Id: 99 , Name: David Id: 23 ]

A level by level listing of the heap:
Level 1:
1000

Level 2:
72
99
900

Level 3:
20
-100
54
-10
66
84
40

'''

9.2. Figures from Text

Fig. 1: Heap Shape

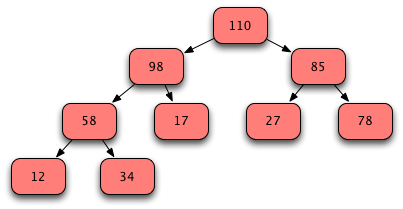
Fig. 2: Sample Heap

Fig. 3: Heap Organization

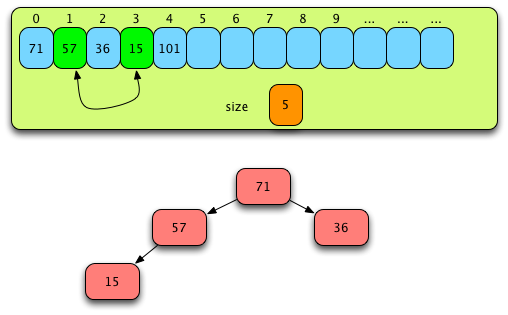
Fig. 4: Building a Heap Part One

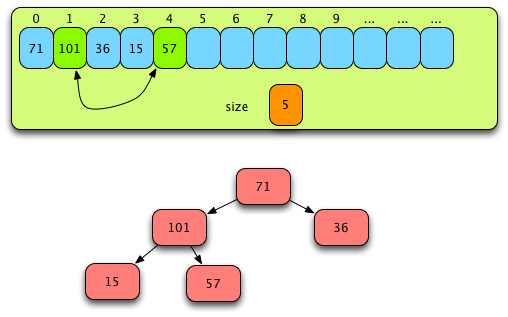
Fig. 5: Building a Heap Part Two

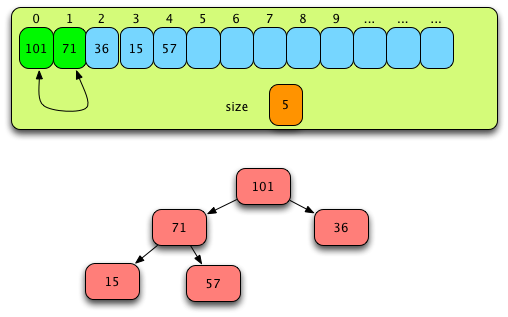
Fig. 6: Building a Heap Part Three

Fig. 7: Adding 98 to the Heap

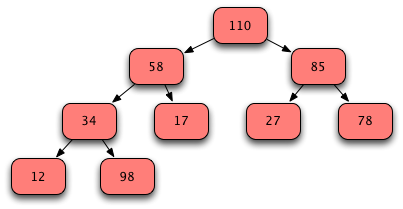
Fig. 8: Conceptual View While Adding 98 to the Heap

Fig. 9: Heap After Moving 98 to Correct Location

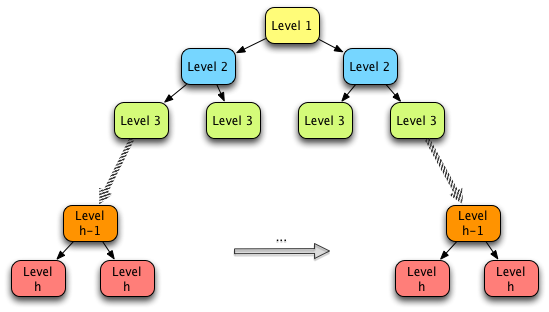
Fig. 10: A Perfect Binary Tree

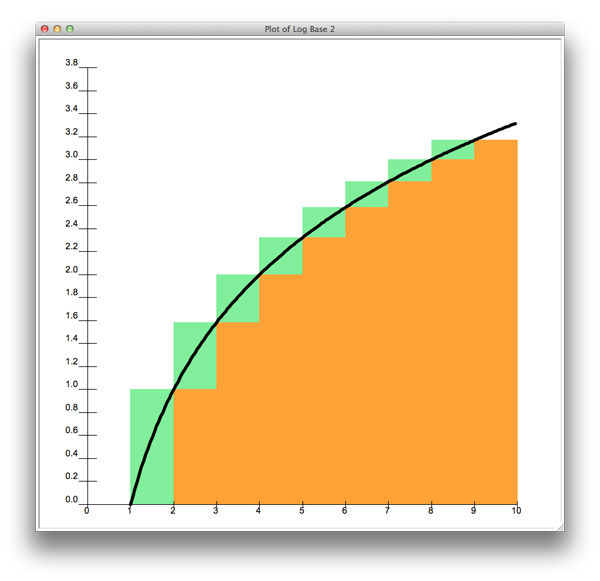
Fig. 11: Plot of log(n)

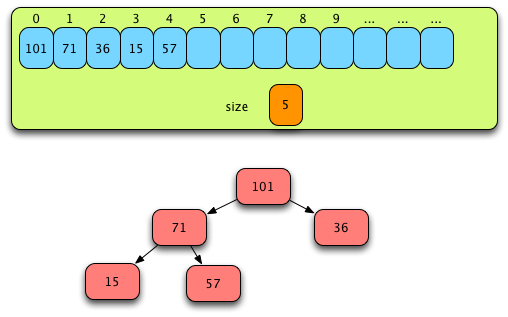
Fig. 12: Just Before Phase II

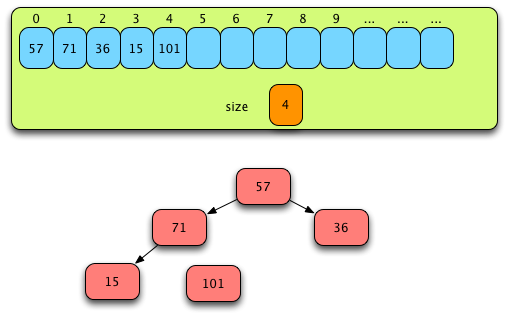
Fig. 13: After Swapping First and Last Values

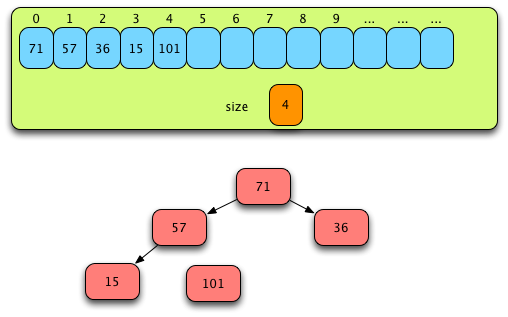
Fig. 14: After the First Pass of Phase II

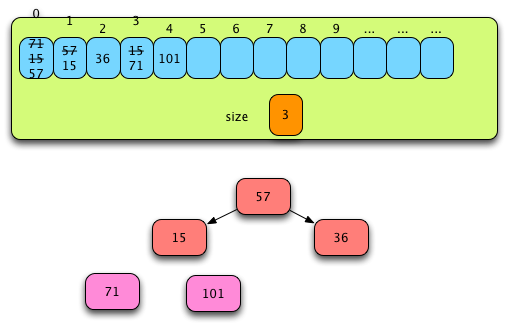
Fig. 15: After the Second Pass of Phase II

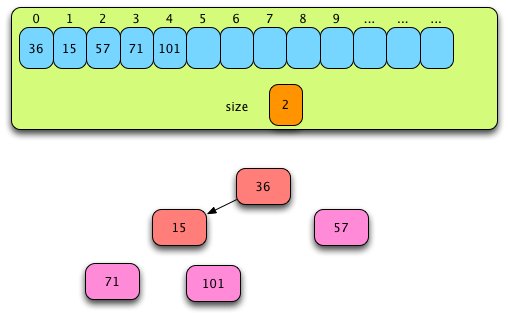
Fig. 16: After the Third Pass of Phase II

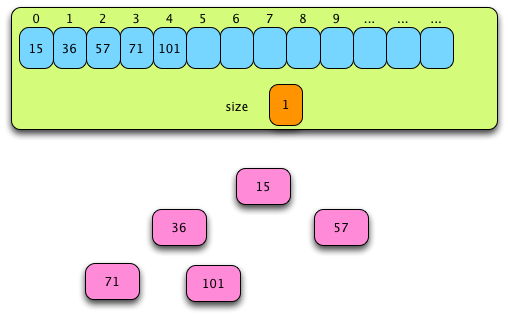
Fig. 17: After the Fourth and Final Pass of Phase II

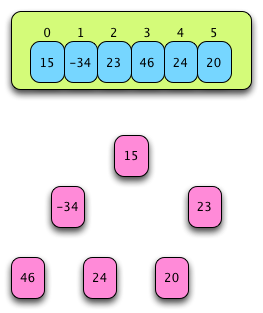
Fig. 18: A List to be Heapsorted

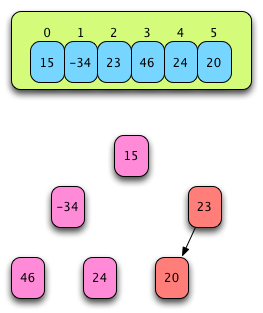
Fig. 19: After Forming a Sub-Heap

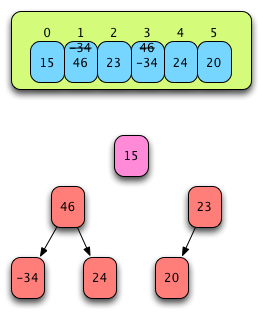
Fig. 20: After Forming a Second Sub-Heap

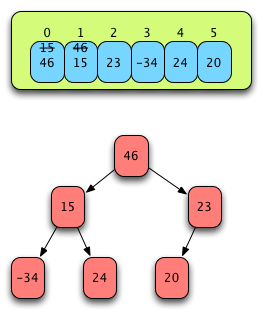
Fig. 21: Sifting the 15 Down

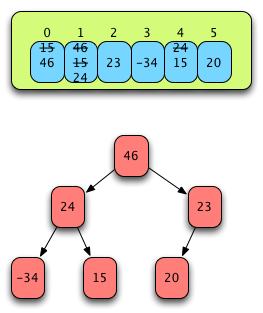
Fig. 22: The Final Heap using Version 2 of Phase I

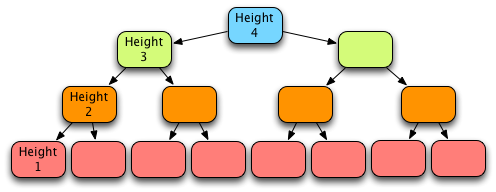
Fig. 23: A Binary Heap of Height 4

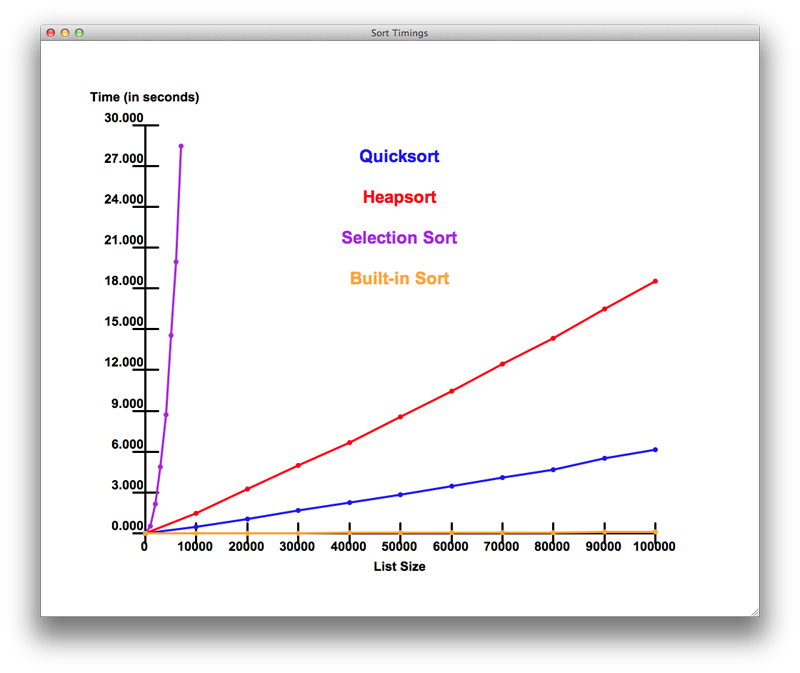
Fig. 24: Comparison of Several Sorting Algorithms