3. Recursion

Don’t think too hard! That’s one of the central themes of this chapter. It’s not often that you tell computer programmers not to think too hard, but this is one time when it is appropriate. You need to read this chapter if you have not written recursive functions before. Most computer science students start by learning to program in a style called imperative programming. This simply means that you are likely used to thinking about creating variables, storing values, and updating those values as a program proceeds. In this chapter you are going to begin learning a different style of programming called functional programming. When you program in the functional style, you think much more about the definition of what you are programming than how you are going to program it. Some say that writing recursive functions is a declarative approach rather than an imperative approach. You’ll start to learn what that means for you very soon. When you start to get good at writing recursive functions you’ll be surprised how easy it can be!

3.1. Scope

You can download the program by clicking here.

import math


PI = math.pi

def area(radius):
    global z
    z = 6
    theArea = PI * radius ** 2
    
    return theArea


def main():
    global z
    
    historyOfPrompts = []
    historyOfOutput = []
    
    def getInput(prompt):
        x = input(prompt)
        historyOfPrompts.append(prompt)
        
        return x
    
    def showOutput(val):
        historyOfOutput.append(val)
        print(val)
    
    rString = getInput("Please enter the radius of a circle: ")
    
    r = float(rString)
    
    val = area(r)
    print(z)
    showOutput("The area of the circle is " + str(val))
    
if __name__ == "__main__":
    main()

3.2. Recursive Spiral

You can download the program by clicking here.

import turtle

def drawSpiral(t, length, color, colorBase):
    #color is a 24 bit value that is changing a bit
    #each time for a nice color effect
    if length == 0:
        return
    
    # add 2^10 to the old color modulo 2^24 
    # the modulo 2^24 prevents the color from 
    # getting too big.
    newcolor = (int(color[1:],16) + 2**10)%(2**24)
    
    # find the color base integer value
    base = int(colorBase[1:],16)
    
    # now if the new color is less than the base
    # add the base module 2^24.
    if newcolor < base:
        newcolor = (newcolor + base)%(2**24)
     
    # let newcolor be the hex string after conversion.   
    newcolor = hex(newcolor)[2:]
    
    # add a pound sign and zeroes to the front so it
    # is 6 characters long plus the pound sign for a
    # proper color string. 
    newcolor = "#"+("0"*(6-len(newcolor)))+newcolor

    t.color(newcolor)   
    t.forward(length)   
    t.left(90)
    
    drawSpiral(t, length-1, newcolor, colorBase)
        
def main():
    t = turtle.Turtle()
    screen = t.getscreen()
    t.speed(100)
    t.penup()
    t.goto(-100,-100)
    t.pendown()

    drawSpiral(t, 200, "#000000", "#ff00ff")
    
    screen.exitonclick()
    

if __name__ == "__main__":
    main()
        

3.3. Sunflower Program

You can download the program by clicking here.

This program is not included in the text, but is a good program to look at when starting chapter 3. It illustrates the golden rule and the fibonacci sequence. Computing fibonacci numbers both recursively and iteratively can lead to a good discussion of computational complexity as well as recursion. You can write a program to time computing fibonacci numbers both recursively and iteratively. The recursive version will not handle numbers bigger than 20 or so. The iterative version can go very high. It is interesting to look at the graph of these two methods of computing fibonacci numbers as a contrast in what is efficient and what is not.

''' 
    Author: Kent D. Lee
    Date: 9/26/2014
    Copyright (c) 2014
    Free for educational use. Others may use with permission.

    Source: 

    I used http://fractalfoundation.org/OFC/OFC-11-3.html as a source for this 
    information. 
    
    Description:
    
    This program draws sunflower seeds in the pattern of a funflower. The ration of 
    consecutive fibonacci numbers in the sequence approach the golden ratio as the 
    sequence grows. In the limit, the ratio of two consecutive fibonacci numbers is
    the golden ratio. 
    
    In the sunflower fibonacci numbers can be observed by counting the number of seeds
    in the spiral arms. Count the number of seeds in a left spiral arm and a right spiral
    arm. You'll see that they are two fibonacci numbers. 
    
    You may have to make the radius size of the seeds constant to count the seeds. It won't
    look as pretty, but will be easier to count. You may also need to increase the forward 
    to separate the seeds. 
'''

import turtle
import math


class Circle:
    def __init__(self,radius, width=1,color="white",outline="black"):
        self.radius = radius
        self.width = width
        self.color = color
        self.outline = outline
        
    def draw(self,turtle):
        centerX = turtle.xcor()
        centerY = turtle.ycor()
        turtle.penup()
        turtle.goto(centerX+self.radius,centerY)
        turtle.pendown()
        turtle.width(self.width)
        turtle.pencolor(self.outline)
        turtle.fillcolor(self.color)
        turtle.begin_fill()
        for i in range(361):
            newX = self.radius * math.cos((i/180.0) * math.pi) + centerX
            newY = self.radius * math.sin((i/180.0) * math.pi) + centerY
            turtle.goto(newX,newY)
            
        turtle.end_fill()
        turtle.penup()
        turtle.goto(centerX, centerY)
        turtle.pendown()
        
def main():
    
    t = turtle.Turtle()
    t.ht()
    screen = t.getscreen()
    screen.tracer(0)
    
    for x in range(400):
        c = Circle(x/16+4,width=2,color="yellow")
        c.draw(t)
        # This angle is chosen because it is approx.
        # 360/1.61803399. The 1.61803399 is the approx.
        # value of the golden angle
        t.left(222.5)
        t.penup()
        t.forward(x*2 + 8)
        screen.update()
    
    
    
    screen.exitonclick()
    
if __name__ == "__main__":
    main()

3.4. Figures from Text

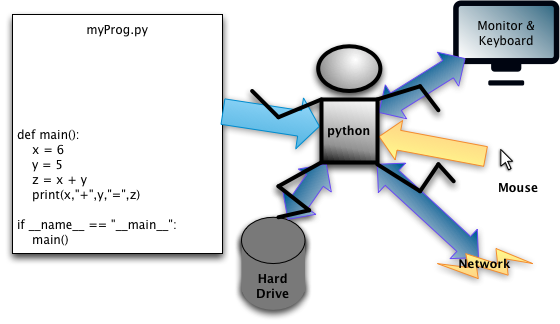
Fig. 1: The Python Interpreter

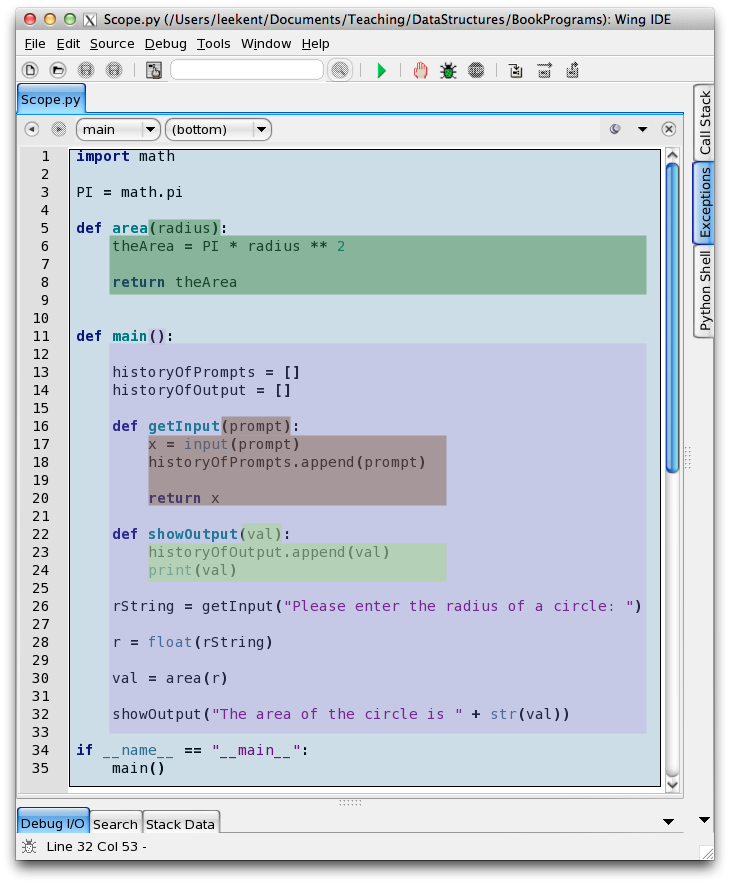
Fig. 2: Scopes within a Simple Program

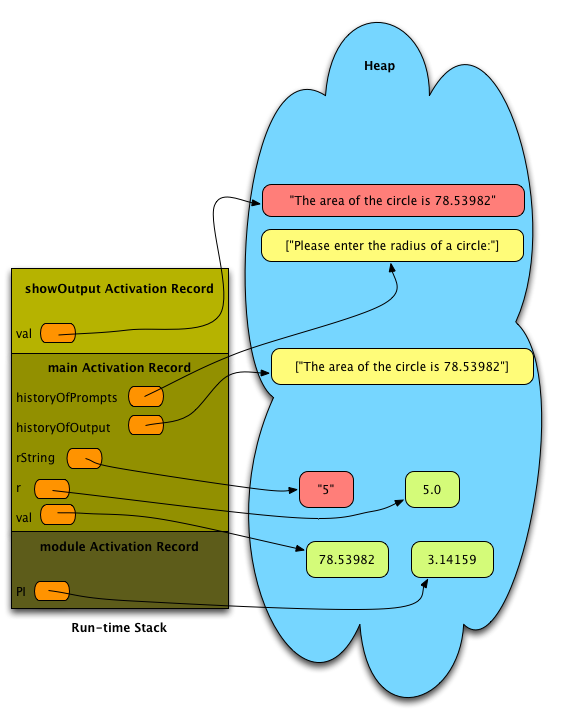
Fig. 3: The Run-time Stack and the Heap

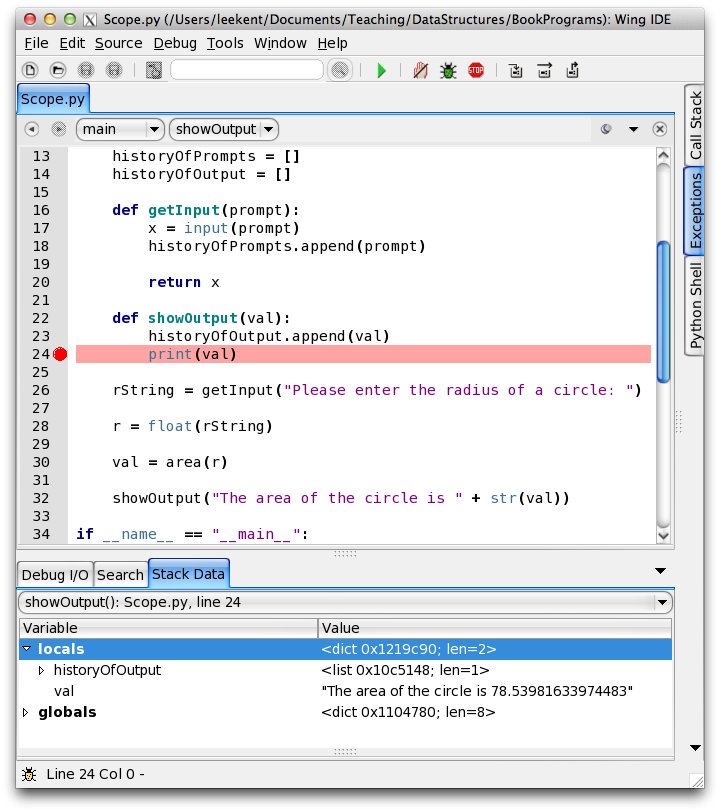
Fig. 4: The Wing IDE Showing the Run-time Stack

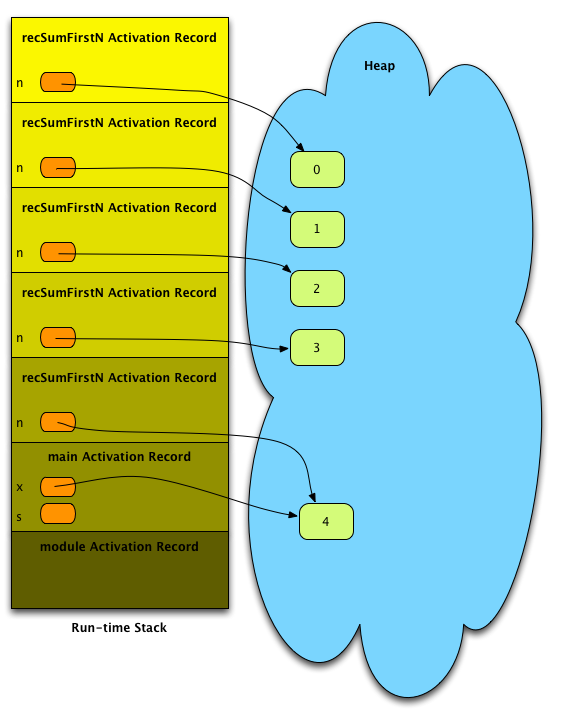
Fig. 5: The Run-time Stack of a Recursive Function Call

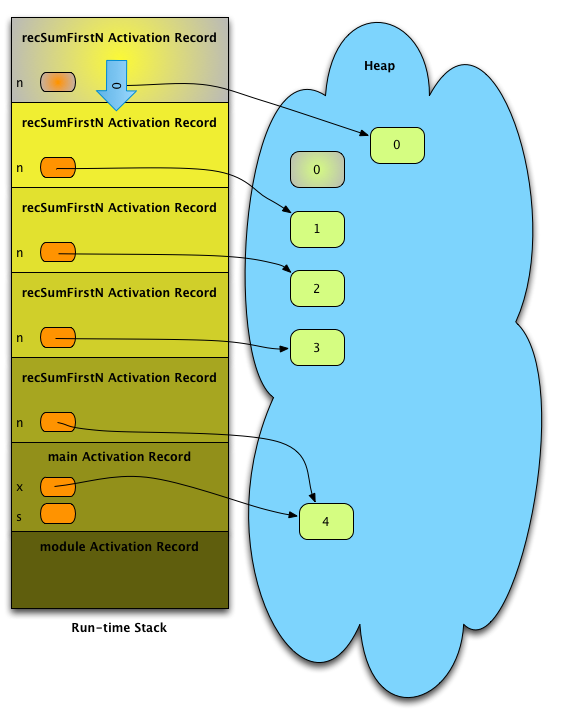
Fig. 6: The First Return from recSumFirstN

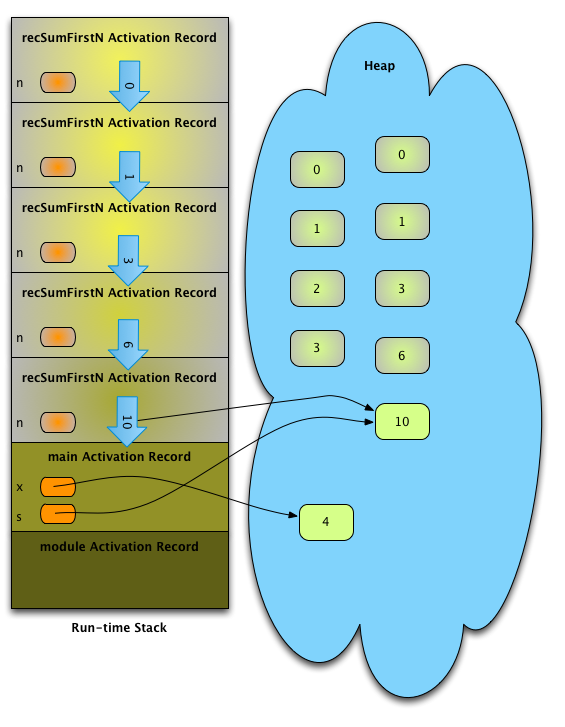
Fig. 7: The Last Return from recSumFirstN

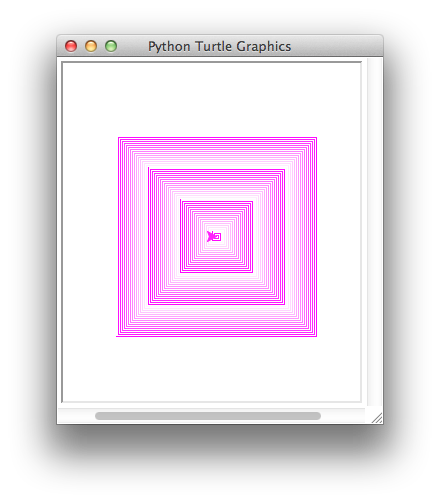
Fig. 8: A Spiral Image

Fig. 9: A Tree