8. Type Inference¶
8.1. Why Static Type Inference?¶
1 2 3 4 5 | let val x = ref 0
in
x := !x + 1;
println (!x)
end
|
Fig 8.1 test8.sml
1 2 3 4 5 | let val x = ref 0
in
x := x + 1;
println (x)
end
|
Fig 8.2 test13.sml
1 2 3 4 5 6 7 8 9 10 11 | exception E of int;
fun g(y) = raise E(y);
fun f(x) =
let
exception E of real;
fun z(y)= raise E(y);
in
x(3.0);
z(3)
end;
f(g);
|
Fig. 8.3 Exception Program
stdIn:216.8-216.12 Error: operator and operand don't agree [literal]
operator domain: real
operand: int
in expression:
z 3
1 2 3 4 5 | let val x = 6
in
println x
println "Done"
end
|
Fig 8.4 A bad function call
8.3. Using Prolog¶
letdec( bindval(idpat('x'),apply(id('ref'),int('0'))), [apply(id(':='),tuple([id('x'), apply(id('+'),tuple([apply(id('!'),id('x')), int('1')]))])), apply(id('println'),apply(id('!'),id('x'))) ]).
Fig. 8.5 test8.sml prolog AST
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | finalStatus(typeerror) :- print('The program failed to pass the typechecker.'), nl, !.
finalStatus(_) :- print('The program passed the typechecker.'), nl, !.
warning([],_) :- !.
warning(_,fn(_,_)) :- !.
warning([_|_],_) :-
print('Warning: type vars not instantiated in result type initialized to dummy types!'),
nl, nl, !.
errorOut(error(E)) :-
nl, nl, print('Error: Typechecking failed. Message was : '), nl,
print(E), nl, nl, halt(0).
errorOut(typeerror(E)) :-
nl, nl, print('Error: Typechecking failed due to type error. Message was : '), nl,
print(E), nl, nl, halt(0).
errorOut(E) :-
nl, nl, print('Error: Typechecking failed for unknown reason : '), nl,
print(E), nl, nl, halt(0).
run :- print('Typechecking is commencing...'), nl,
readAST(AST), print('Here is the AST'), nl, print(AST), nl, nl, nl,
catch(typecheckProgram(AST,Type),E,errorOut(E)),
nl, nl, print('val it : '), printType(Type,TypeVars), nl, nl,
warning(TypeVars,Type), finalStatus(Type).
runNonInteractive :- run, halt(0).
|
Fig. 8.6 The Type Checker run Predicate
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | datatype
exp = int of string
| ch of string
| str of string
| bool of string
| id of string
| listcon of exp list
| tuplecon of exp list
| apply of exp * exp
| expsequence of exp list
| letdec of dec * (exp list)
| handlexp of exp * match list
| ifthen of exp * exp * exp
| whiledo of exp * exp
| func of string * match list
and
match = match of pat * exp
and
pat = intpat of string
| chpat of string
| strpat of string
| boolpat of string
| idpat of string
| wildcardpat
| infixpat of string * pat * pat
| tuplepat of pat list
| listpat of pat list
| aspat of string * pat
and
dec = bindval of pat * exp
| bindvalrec of pat * exp
| funmatch of string * match list
| funmatches of (string * match list) list
|
Fig. 8.7 AST Description
type = bool
| int
| str
| exn
| tuple of type list
| listOf of type
| fn of type * type
| ref of type
| typevar of string
| typeerror
Fig. 8.8 Small Types
8.4. The Type Environment¶
typecheckProgram(Expression,Type) :-
typecheckExp([('Exception',fn(typevar(a),exn)),
('raise',fn(exn,typevar(a))),
('andalso',fn(tuple([bool,bool]),bool)),
('orelse',fn(tuple([bool,bool]),bool)),
(':=',fn(tuple([ref(typevar(a)),typevar(a)]),tuple([]))),
('!',fn(ref(typevar(a)),typevar(a))),
('ref',fn(typevar(a),ref(typevar(a)))),
('::',fn(tuple([typevar(a),listOf(typevar(a))]),listOf(typevar(a)))),
('>', fn(tuple([typevar(a),typevar(a)]),bool)),
('<', fn(tuple([typevar(a),typevar(a)]),bool)),
(@,fn(tuple([listOf(typevar(a)),listOf(typevar(a))]),listOf(typevar(a)))),
('Int.fromString',fn(str,int)),
('input',fn(str,str)),
('explode',fn(str,listOf(str))),
('implode',fn(listOf(str),str)),
('println',fn(typevar(a),tuple([]))),
('print',fn(typevar(a),tuple([]))),
('cprint',fn(typevar(a),cprint)),
('type',fn(typevar(a), str)),
(+,fn(tuple([int,int]),int)),
(-,fn(tuple([int,int]),int)),
(*,fn(tuple([int,int]),int)),
('div',fn(tuple([int,int]),int))],
Expression,Type).
Fig. 8.9 The Prolog Type Environment
8.5. Integers, Strings, and Boolean Constants¶
typecheckExp(_,int(_),int).
typecheckExp(_,bool(_),bool).
typecheckExp(_,str(_),str).
Fig. 8.10 Constant Types
BoolCon
IntCon
StringCon
8.5.1. Example 8.1¶
Typechecking is commencing...
Here is the AST
int(5)
val it : int
The program passed the typechecker.
8.6. List and Tuple Constants¶
typecheckExp(Env,listcon(L),listOf(T)) :- typecheckList(Env,L,T).
typecheckExp(Env,tuple(L),tuple(T)) :- typecheckTuple(Env,L,T).
listOf(int)
tuple([str,bool,int])
ListCon
TupleCon
8.6.1. Example 8.2¶
Typechecking is commencing...
Here is the AST
listcon([int(1),int(2),int(3),int(4)])
val it : int list
The program passed the typechecker.
8.7. Identifiers¶
1 2 3 4 5 6 7 8 9 10 11 | exists(Env,Name) :-
member((Name,_),Env), !.
find(Env,Name,Type) :-
member((Name,Type),Env), !.
find(Env,Name,Type) :-
writeMsg(['Failed to find ',
Name,' with type ',Type,
' in environment : ']), print(Env), nl,
throw(typeerror('unbound identifier')).
typecheckExp(Env,id(Name),Type) :-
find(Env,Name,Type).
|
Fig. 8.11 Environment Lookup Predicates
Identifier
8.7.1. Example 8.3¶
Typechecking is commencing...
Here is the AST
id(println)
val it : 'a -> unit
The program passed the typechecker.
8.8. Function Application¶
println 6
FunApp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | instanceOfList(Env,[],[],Env).
instanceOfList(Env,[H|T],[G|S],NewEnv) :-
instanceOf(Env,H,G,Env1), instanceOfList(Env1,T,S,NewEnv).
instanceOf(Env,A,A,Env) :- var(A), !.
instanceOf(Env,A,A,Env) :- simple(A), !.
instanceOf(Env,fn(A,B), fn(AInst,BInst),Env2) :-
instanceOf(Env,A,AInst,Env1), instanceOf(Env1,B,BInst,Env2), !.
instanceOf(Env,listOf(A),listOf(B),NewEnv) :- instanceOf(Env,A,B,NewEnv), !.
instanceOf(Env,ref(A),ref(B),NewEnv) :- instanceOf(Env,A,B,NewEnv), !.
instanceOf(Env,tuple(L),tuple(M),NewEnv) :- instanceOfList(Env,L,M,NewEnv), !.
instanceOf(Env,typevar(A),B,Env) :- exists(Env,A), find(Env,A,B), !.
instanceOf(Env,typevar(A),B,[(A,B)|Env]) :- !.
instanceOf(_,A,B,_) :-
print('Type Error: Type '), printType(B,_),
print(' is not an instance of '), printType(A,_), nl,
throw(typeerror('type mismatch')), !.
inst(X,Y) :- instanceOf([],X,Y,_).
|
Fig. 8.12 The Instantiation Operator
typecheckExp(Env,apply(Exp1,Exp2),ITT) :-
typecheckExp(Env,Exp1,fn(FT,TT)), typecheckExp(Env,Exp2,Exp2Type),
inst(Exp2Type,Exp2TypeInst), catch(inst(fn(FT,TT), fn(Exp2TypeInst,ITT)),_,
printApplicationErrorMessage(Exp1,fn(FT,TT),Exp2,Exp2Type,ITT)), !.
Fig. 8.13 Function Application Type Inference
8.8.1. Instantiation¶
8.8.2. Example 8.4¶
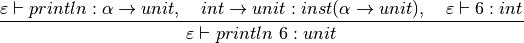
8.10. Patterns¶
IntPat
BoolPat
StrPat
NilPat
ConsPat
TuplePat
ListPat
let
val (x,y)::L = [(1,2),(3,4)]
in
println x
end
Fig. 8.14 Pattern Matching
IdPat
8.10.1. Example 8.6¶
letdec(
bindval(infixpat(::,tuplepat([idpat(x),idpat(y)]),idpat(L)),
listcon([tuple([int(1),int(2)]),tuple([int(3),int(4)])])),
[apply(id(println),id(x))])
val (x,y)::L : (int * int) list
val it : unit
The program passed the typechecker.
![\dfrac{
(2) \varepsilon\vdash val~(x,y)::L = [(1,2),(3,4)]\Rightarrow\varepsilon_{dec}
~~~
(3) \varepsilon_{dec}\oplus\varepsilon\vdash println~x : unit
}{
(1)\varepsilon\vdash let~val~(x,y)::L = [(1,2),(3,4)]~in~println~x~end : unit
}(Let)
\varepsilon_{dec} =[x\mapsto int, y\mapsto int, L\mapsto int * int~list]](_images/math/f161013f47989eb932b33cdfcdabaf99b19de24c.png)
To prove (2):
![\dfrac{
(4) (x,y)::L : int\times int~list\Rightarrow\varepsilon_{dec}
~~~
(5) \varepsilon\vdash [(1,2),(3,4)] : int\times int~list
}{
(2) \varepsilon\vdash val~(x,y)::L = [(1,2),(3,4)]\Rightarrow\varepsilon_{dec}
}(ValDec)](_images/math/a27224e7c8cf69e22eef758eb6d7ed797c621960.png)
To prove (4):
![\dfrac{
(6) (x,y) : int \times int \Rightarrow [x\mapsto int, y\mapsto int]
~~~
(7) L : int\times int~list \Rightarrow[L\mapsto int\times int~list]
}{
(4) (x,y)::L : int\times int~list\Rightarrow\varepsilon_{dec}
}(ConsPat)](_images/math/9f10c75eeff0bdaeb3b28e28c883835fd1e39f99.png)
To prove (6):
![\dfrac{
(8) x : int \Rightarrow[x\mapsto int]
~~~
(9) y : int \Rightarrow[y\mapsto int]
}{
(6) (x,y) : int \times int \Rightarrow [x\mapsto int, y\mapsto int]
}(TuplePat)](_images/math/c8a24233b25e185403d32797914fe559b033c87a.png)
Premises (7), (8), and (9) are true by virtue of the IdPat inference rule. Considering (5):
![\dfrac {
(10)\varepsilon\vdash (1,2):int\times int
~~~
(11)\varepsilon\vdash (3,4):int\times int
}{
(5) \varepsilon\vdash [(1,2),(3,4)] : int\times int~list
}(ListCon)](_images/math/8122e2c401b8181e6c2df7aa815f75807d9f7e84.png)
Considering (10) and a similar argument for (11):
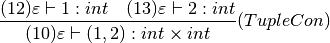
Both (12) and (13) are true by the IntCon rule. A similar argument holds for (11). The proof nears completion by proving (3):
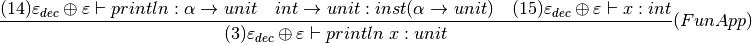
Both (14) and (15) are true by the Identifier rule concluding the proof of the type correctness of this program.
let val x = 5
val y = 6
in
println (x + y)
end
Fig. 8.15 test10.sml
Practice 8.1
Prove that the program given in figure 8.13 is correctly typed. The abstract syntax for this program is provided here.
letdec(bindval(idpat('x'),int('5')), [letdec(bindval(idpat('y'),int('6')), [apply(id('println'),apply(id('+'),tuple([id('x'),id('y')])))]) ]).
Practice 8.2
Minimally, what must the type environment contain to correctly type check the program in figure 8.15.
8.11. Matches¶
let fun f(0,y) = y
| f(x,y) = g(x,x*y)
and g(x,y) = f(x-1,y)
in
println (f(10,5))
end
Fig. 8.16 test11.sml
Matches
or
8.11.1. Example 8.7¶
letdec(
funmatches(
[funmatch(f,
[match(tuplepat([intpat(0),idpat(y)]),id(y)),
match(tuplepat([idpat(x),idpat(y)]),apply(id(g),
tuple([id(x),apply(id(*),tuple([id(x),id(y)]))])))]),
funmatch(g,
[match(tuplepat([idpat(x),idpat(y)]),
apply(id(f),tuple([apply(id(-),tuple([id(x),int(1)])),id(y)])))])]),
[apply(id(println),apply(id(f),tuple([int(10),int(5)])))])
8.12. Anonymous Functions¶
(fn x => x+1)
Fig. 8.17 Anonymous Function
- AnonFun
![\frac{[id\mapsto\alpha\rightarrow\beta]\oplus\varepsilon\vdash id~matches:\alpha\rightarrow\beta}
{\varepsilon\vdash fn~id~matches:\alpha\rightarrow\beta}](_images/math/30124b774db27143be378caa4a2c38e7be81836b.png)
8.12.1. Example 8.8¶
func(anon@0,[match(idpat(x),apply(id(+),tuple([id(x),int(1)])))])
Practice 8.3
Provide a complete proof that the program in figure 8.17 is correctly typed.
8.14. If-Then and While-Do¶
IfThen
WhileDo
typecheckExp(Env,ifthen(Exp1,Exp2,Exp3), RT) :-
typecheckExp(Env,Exp1,bool), typecheckExp(Env,Exp2,RT), typecheckExp(Env,Exp3,RT), !.
typecheckExp(Env,ifthen(Exp1,Exp2,Exp3), _) :-
typecheckExp(Env,Exp1,bool), typecheckExp(Env,Exp2,ThenType), typecheckExp(Env,Exp3,ElseType),
print('Error: Result types of then and else expressions must match.'), nl,
print('Then Expression type is: '), printType(ThenType,_), nl,
print('Else Expression type is: '), printType(ElseType,_), nl,
throw(typeerror('result type mismatch in if-then-else expression')).
typecheckExp(Env,ifthen(Exp1,_,_), _) :-
typecheckExp(Env,Exp1,Exp1Type), Exp1Type \= bool,
print('Error: Condition of if then expression must have bool type.'), nl,
print('Condition Expression type was: '), printType(Exp1Type,_), nl,
throw(typeerror('type not bool in if-then-else expression condition')).
Fig. 8.18 If-Then Prolog Code
8.16. Chapter Summary¶
8.17. Review Questions¶
What appears above and below the line in a type inference rule?
Why don’t infix operators appear in the abstract syntax of programs handled by the type checker?
What does typevar represent in figure 8.6?
What does typeerror represent in figure 8.6?
What does the type of the list [(“hello”,1,true)] look like as a Prolog term?
What is the type environment?
Give an example of the use of the overlay operator.
What pattern(s) are used in this let expression?
let val (x,y,z) = ("hello",1,true) in println x end
What is the pattern as a Prolog term?
Give an example where the Sequence rule might be used to infer a type.
Give a short example of where the Handler rule might be used to infer a type.
8.18. Exercises¶
The following program does not compile correctly or typecheck correctly using the mlcomp compiler and type inference system. However, it is a valid Standard ML program. Modify both the mlcomp compiler and type checker to correctly compile and infer its type. This program is included in the compiler project as test20.sml.
let val [(x,y,z)] = [(l+s+s2{h}ellop{,}1,true)] in println x end
Output from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(bindval(listpat([tuplepat([idpat(x),idpat(y),idpat(z)])]), listcon([tuple([str("hello"),int(1),bool(true)])])), [apply(id(println),id(x))]) val [(x,y,z)] : (str * int * bool) list val it : unit The program passed the typechecker.
Implement the Prolog type predicates to get the following program to type check successully. This program is test14.sml in the mlcomp compiler project. This will involve writing type checking predicates for matching, boolean patterns, integer patterns, and sequential execution.
let fun f(true,x) = (println(x); g(x-1)) | f(false,x) = g(x-1) and g 0 = () | g x = f(true,x) in g(10) end
Output from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(funmatches([funmatch(f,[match(tuplepat([boolpat(true),idpat(x)]), expsequence([apply(id(println),id(x)),apply(id(g),apply(id(-), tuple([id(x),int(1)])))])),match(tuplepat([boolpat(false),idpat(x)]), apply(id(g),apply(id(-),tuple([id(x),int(1)]))))]),funmatch(g,[match(intpat(0), tuple([])),match(idpat(x),apply(id(f),tuple([bool(true),id(x)])))])]), [apply(id(g),int(10))]) val f = fn : bool * int -> unit val g = fn : int -> unit val it : unit The program passed the typechecker.
Implement enough of the type checker to get test12.sml to type check correctly. This will mean writing the WhileDo inference rule as a Prolog predicate, implementing the Match rule’s predicate called typecheckMatch, and the type inference predicate for sequential execution named typecheckSequence as defined in the Sequence rule. The code for test12.sml is given here for reference.
let val zero = 0 fun fib n = let val i = ref zero val current = ref 0 val next = ref 1 val tmp = ref 0 in while !i < n do ( tmp := !next + !current; current := !next; next := !tmp; i := !i + 1 ); !current end val x = Int.fromString(input(l+s+s2{"lease enter an integer: ")) val r = fib(x) in print l+s+s2{F}ib(p{;} print x; print l+s+s2{)} is p{;} println r endOutput from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(bindval(idpat(zero),int(0)),[letdec(funmatches([funmatch(fib, [match(idpat(n),letdec(bindval(idpat(i),apply(id(ref),id(zero))), [letdec(bindval(idpat(current),apply(id(ref),int(0))), [letdec(bindval(idpat(next),apply(id(ref),int(1))), [letdec(bindval(idpat(tmp),apply(id(ref),int(0))), [whiledo(apply(id(<),tuple([apply(id(!),id(i)),id(n)])), expsequence([apply(id(:=),tuple([id(tmp),apply(id(+),tuple([apply(id(!),id(next)), apply(id(!),id(current))]))])),apply(id(:=),tuple([id(current),apply(id(!), id(next))])),apply(id(:=),tuple([id(next),apply(id(!),id(tmp))])),apply(id(:=), tuple([id(i),apply(id(+),tuple([apply(id(!),id(i)),int(1)]))]))])),apply(id(!), id(current))])])])]))])]),[letdec(bindval(idpat(x),apply(id(Int.fromString), apply(id(input),str("Please enter an integer: ")))), [letdec(bindval(idpat(r),apply(id(fib),id(x))),[apply(id(print),str("Fib(")), apply(id(print),id(x)),apply(id(print),str(") is ")),apply(id(println),id(r))])])])]) val zero : int val i : int ref val current : int ref val next : int ref val tmp : int ref val fib = fn : int -> int val x : int val r : int val it : unit The program passed the typechecker.Add support to the type checker to correctly infer the types of case expressions in Small. The following program should type check correctly once this project is completed. This test is in test15.sml in the mlcomp compiler project. This will involve writing code to correctly type check matches according to the Match rule. If case statments are not yet implemented in the compiler, support must be added to the compiler to parse case expressions, build an AST for them, and write their AST to the a.term file.
let val x = 4 in println (case x of 1 => "hello" | 2 => "how" | 3 => "are" | 4 => "you") end
Output from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(bindval(idpat(x),int(6)),[apply(id(println),caseof(id(x), [match(intpat(1),str("hello")),match(intpat(2),str("how")), match(intpat(3),str("are")),match(intpat(4),str("you"))]))]) val x : int val it : unit The program passed the typechecker.
Add support to the type checker to correctly infer the types for test7.sml. The code is provided below for reference. Support will need to be added to infer the types of anonymous functions defined in the rule AnonFun, matching defined in the rule Matches, and the ConsPat rule.
let fun append nil L = L | append (h::t) L = h :: (append t L) fun appendOne x = (fn nil => (fn L => L) | h::t => (fn L => h :: (appendOne t L))) x in println(append [1,2,3] [4]); println(appendOne [1,2,3] [4]) end
Output from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(funmatches([funmatch(append,[match(idpat(v0),func(anon@3, [match(idpat(v1),apply(func(anon@2,[match(tuplepat([idpat(nil),idpat(L)]),id(L)), match(tuplepat([infixpat(::,idpat(h),idpat(t)),idpat(L)]),apply(id(::), tuple([id(h),apply(apply(id(append),id(t)),id(L))])))]), tuple([id(v0),id(v1)])))]))])]),[letdec(funmatches([funmatch(appendOne, [match(idpat(x),apply(func(anon@6,[match(idpat(nil),func(anon@4, [match(idpat(L),id(L))])),match(infixpat(::,idpat(h),idpat(t)), func(anon@5,[match(idpat(L),apply(id(::),tuple([id(h),apply(apply(id(appendOne),id(t)), id(L))])))]))]),id(x)))])]),[apply(id(println),apply(apply(id(append), listcon([int(1),int(2),int(3)])),listcon([int(4)]))),apply(id(println), apply(apply(id(appendOne),listcon([int(1),int(2),int(3)])),listcon([int(4)])))])]) val append = fn : 'a list -> 'a list -> 'a list val appendOne = fn : 'a list -> 'a list -> 'a list val it : unit The program passed the typechecker.
Add support for type inference for recursive bindings. The following program, saved as test19.sml in the Small compiler project, is a valid program with a recursive binding. It will type check correctly if the ValRecDec type inference rule is implemented. Write the code to get this program to pass the type checker as a valid program.
let val rec f = (fn 0 => 1 | x => x * (f (x-1))) in println(f 5) end
Output from the type checker should appear as follows.
Typechecking is commencing... Here is the AST letdec(bindvalrec(idpat(f),func(anon@0,[match(intpat(0),int(1)),match(idpat(x), apply(id(*),tuple([id(x),apply(id(f),apply(id(-),tuple([id(x),int(1)])))])))])), [apply(id(println),apply(id(f),int(5)))]) val f = fn : int -> int val it : unit The program passed the typechecker.
Currently the type checker allows duplicate identifiers in compound patterns like listPat and tuplePat. Standard ML does not allow duplicate identifiers in patterns. The type checker uses the append predicate to combine pattern binding environments. This is not good enough. Find the locations in the type checker where pattern environments are incorrectly appended and rewrite this code to enforce that all identifiers within a pattern must be unique. If not, you should print an error message like “Error: duplicate variable in pattern(s): x” to indicate the problem and typechecking should end with an error.
Currently, the abstract syntax and parser of Small includes support for the wildcard pattern in pattern matching, but the type checker does not support it. Add support for wildcard patterns, write a test program, and test the compiler and type checker. Be sure to write a type inference rule for wildcard patterns first.
Currently, the abstract syntax and parser of Small includes support for the as pattern in pattern matching, but the type checker does not support it. Add support for as patterns, write a test program, and test the compiler and type checker. The as pattern comes up when you write a pattern like L as h::t which assigns L as a pattern that represents the same value as the compound pattern of h::t. Be sure to write a type inference rule for as patterns first.
8.19. Solutions to Practice Problems¶
8.19.1. Solution to Practice Problem 8.1¶
The complexity of append is O(n) in the length of the first list.
8.19.2. Solution to Practice Problem 8.2¶
Minimally the environment must contain println bound to a function
type of 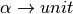 and the + function bound to a
function type of
and the + function bound to a
function type of 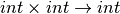 .
.
8.19.3. Solution to Practice Problem 8.3¶
The AnonFun rule is applied first which requires the Matches rule be applied. The Matches rule requires the use of the IdPat rule and the FunApp rule. Finally, the IntCon rule is needed to complete the proof.

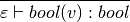
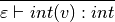
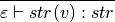
![[ 6, 5, 4 ] & : int~~list \\
( "hi", true, 6) & : str * bool * int](_images/math/01037277a5ff86c8093a064b508bd911414fbf4a.png)
![& \forall i~~1\leq i \leq n, n \geq 0\\
& \frac{\varepsilon\vdash e_i:\alpha}{\varepsilon\vdash [e_1,e_2,...,e_n] : \alpha~~list}](_images/math/ffe57165cff61bc5c69052daacc2e1007cb0274c.png)
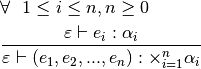
![\frac{}{\varepsilon[id \mapsto \alpha]\vdash id : \alpha}](_images/math/8291394707c5ffe82d6081d7712890eb9b03c026.png)
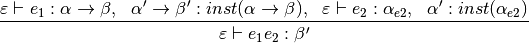
![\varepsilon_1 & = [x\mapsto\alpha\rightarrow\beta,~y\mapsto int,~z\mapsto\alpha\times\beta]\\
\varepsilon_2 & = [u\mapsto\alpha\times\beta\rightarrow\beta,~y\mapsto\ bool]\\
\varepsilon_2\oplus\varepsilon_1 &= [u\mapsto\alpha\times\beta\rightarrow\beta,~y\mapsto\ bool]\oplus[x\mapsto\alpha\rightarrow\beta,~y\mapsto int,~z\mapsto\alpha\times\beta]\\
& = [u\mapsto\alpha\times\beta\rightarrow\beta,~y\mapsto\ bool,x\mapsto\alpha\rightarrow\beta,~y\mapsto int, ~z\mapsto\alpha\times\beta]](_images/math/972bf9fd3d58c96e5c6e033062d4500ea64e7f64.png)
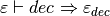
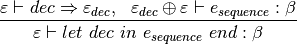
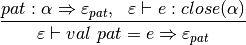
![\frac{[id:\alpha]\oplus\varepsilon\vdash e:\alpha}{\varepsilon\vdash val~rec~id=e\Rightarrow[ id:close(\alpha)]}](_images/math/c7318c5993fce37d8ba1d3ef23a3c2cb3162694f.png)
![& \forall i~1 \leq i \leq n, \forall j~1 < j \leq n,~~n \geq 1,\\
& \frac{[id_1\mapsto\alpha_1\rightarrow\beta_1~\{,~id_j\mapsto\alpha_j\rightarrow\beta_j\}]\oplus\varepsilon\vdash id_i~matches_i:\alpha_i\rightarrow\beta_i}{\varepsilon\vdash f\!un~id_1~matches_1~\{and~id_j~matches_j\}\Rightarrow[id_1\mapsto close(\alpha_1\rightarrow\beta_1)~\{,~id_j\mapsto close(\alpha_j\rightarrow\beta_j)\}]}](_images/math/986b9daa4504b45c12cac0c1db024eae48bcb225.png)
![\frac{}{integer\_constant:int \Rightarrow [~]}](_images/math/0b01d094b3c434b9307f986aae7d68c5aba75535.png)
![& \frac{}{true:bool \Rightarrow [~]} \\
& \frac{}{false:bool \Rightarrow [~]}](_images/math/bc3830a022221a5fe858565e9d89846425a79c20.png)
![\frac{}{string\_constant:str \Rightarrow [~]}](_images/math/d4a668e9a9665903a97e040b648940f10aab32d1.png)
![\frac{}{nil:\alpha~list\Rightarrow[~]}](_images/math/4592d651e7a59b628ad2102ec4c8204005550712.png)
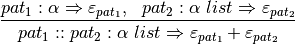
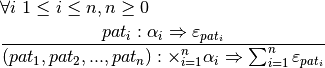
![& \forall i~1 \leq i \leq n, n \geq 0\\
& \frac{pat_i : \alpha \Rightarrow \varepsilon_{pat_i}}
{[pat_1,pat_2,...,pat_n]: \alpha~list\Rightarrow \sum^{n}_{i=1}\varepsilon_{pat_i}}](_images/math/88c9b891056eb2f61ac6a32935f2efd6bad730b6.png)
![\frac{}{id:\alpha\Rightarrow[id\mapsto\alpha]}](_images/math/99f9656dadc13cc8d7a5a19ef073be7abba29c3a.png)
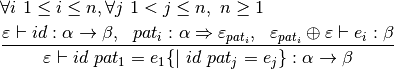
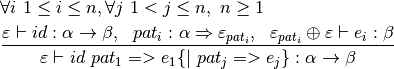
![\frac{[anon@0\mapsto int\rightarrow int]\oplus\varepsilon\vdash anon@0~x => x+1:int\rightarrow int}
{\varepsilon\vdash fn~anon@0~x => x+1 :int\rightarrow int}](_images/math/e579aabb41fb40e295ae1ec6324b4425715bbd3c.png)
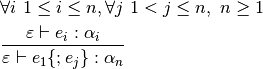
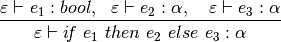
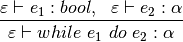
![\frac{\varepsilon\vdash e:\alpha, ~~ [handle@\mapsto~exn\rightarrow\alpha]\oplus\varepsilon\vdash handle@~matches : exn\rightarrow\alpha}
{\varepsilon\vdash e~handle~matches : \alpha}](_images/math/ddb33bbf70ea22e09797118946e45c9a51e1d695.png)