2. Finite Automata

Read all of chapter 2 from Peter Linz’s text, “Formal Languages and Automata”, fifth edition.

2.1. The Ordered Collections

Many of the programs you will write in this course require you to use sets and maps (i.e. dictionaries). As of Python 3.3 the built-in set and dictionary types non-deterministically iterate over their items. None of the algorithms presented here rely on the ordering of items within a set or a dictionary. However, when debugging your code you may want to run your program, then make a modification and run it again to see what happens. But, an ordinary dictionary or set will return a completely different ordering of the items within it, making debugging difficult.

The OrderedMap, OrderedSet, and OrderedFrozenSet classes provided here require an ordering of the keys or items stored in them. However, they also deterministically iterate over those items and keys, returning them in ascending sorted order. You may wish to use these classes in your code. You can save these classes in a file called orderedcollections.py. Then it can be imported for use in your code in the usual way.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class OrderedMap(dict):
    def __init__(self,*args,**kwargs):
        super().__init__(*args, **kwargs)

    def __iter__(self):
        return iter(sorted(super().__iter__()))

class OrderedSet(set):
    def __init__(self,lst=[]):
        super().__init__(lst)

    def __iter__(self):
        return iter(sorted(super().__iter__()))

class OrderedFrozenSet(frozenset):
    def __init__(self,lst=[]):
        self = frozenset(lst)

    def __iter__(self):
        return iter(sorted(super().__iter__()))

2.2. The State Class

The finite state automata in chapter 2 can be modeled with a State class that can be used to construct finite state automata. In the state class below there are classes that are referred to. The classes define classes of characters. For instance, the class letter could be used to represent all characters that are letters, as in a..z and A..Z. So, the classes is a dictionary of class names like letter to sets of ASCII values (i.e. integers). For instance the class letter would map to the set of values 65..90 and 97..122 for all the letters from A to Z, both small and captital. When you build an automaton you should also build this dictionary of classes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
NoTransition = -1

class State:
    def __init__(self, id, acceptsTokenId = None, transitions = {}):
        # An id of -1 is not allowed since that indicates there is
        # no transition on a value.
        if id == -1:
            raise Exception("A state id of -1 is not allowed.")

        self.id = id
        # A copy of the list of transitions needs to be created
        # because Python makes only one instance of a default
        # parameter. Changing the list later, by adding a transition
        # would add that transition to every state. Wow! Talk about
        # bad semantics...
        self.transitions = dict(transitions)
        self.acceptsTokenId = acceptsTokenId

        # This will cause onGoTo to generate an Exception if called
        # before the setClasses method is called.
        self.classes = None

    def setClasses(self, classes):
        self.classes = classes

    def addTransition(self, onClass, toState):
        if onClass in self.transitions:
            raise Exception("Duplicate Transition " + str(onClass) + ". Consider using NFA State instead.")
        self.transitions[onClass] = toState

    def hasTransition(self, onClass):
        return onClass in self.transitions

    def onClassGoTo(self, onClass):
        if self.hasTransition(onClass):
            return self.transitions[onClass]

        return NoTransition

    # You must call setClasses before calling the onGoTo method.
    def onGoTo(self, on):
        for aClass in self.transitions:
            if on in self.classes[aClass]:
                return self.transitions[aClass]

        return NoTransition

    def getTransitions(self):
        return self.transitions

    def getId(self):
        return self.id

    def setAccepting(self, tokenId):
        self.acceptsTokenId = tokenId

    def isAccepting(self):
        return self.acceptsTokenId != None

    def getAcceptsTokenId(self):
        return self.acceptsTokenId

    def __repr__(self):
        return "State(" + repr(self.id) + "," + repr(self.acceptsTokenId) + "," + \
            repr(self.transitions) + ")"

    def __str__(self):
        val = ""
        val = "State " + str(self.id) + "\n"
        if self.acceptsTokenId != None:
            val += "    accepts token with identifier: " + str(self.acceptsTokenId) + "\n"

        for onClass in self.transitions:
            val += "    On " + str(onClass) + " Go To " + str(self.transitions[onClass]) + "\n"

        return val

Fig. 2.1: The Automata State Class - state.py

2.3. JPython Programming Language Example

JPython is a simple programming language similar to Python, but with some Java syntax thrown in. Here is a sample program from this language.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# In JPython you can declare functions and variables.
# Functions are declared/defined with a def keyword.
def factorial(n) {
        if (n == 0)
                return 1;

        # This involves a recursive call. Statements are
        # terminated with semicolons.
        return n * factorial(n-1);
}


def iterativeFactorial(n) {
        # The decl is to declare a local variable.
        decl result = 1;
        for i in range(1,n+1) {
                result = result * i;
        }

        return result;
}

def main() {
        print("The factorial of 5 is", factorial(5));
        print('The iterative factorial of 5 is', iterativeFactorial(5));
}

main();

Fig. 2.2: JPython Sample Program - sample.jpy

2.4. The StreamReader Class

This is the StreamReader class which is useful in reading input and parsing it.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
EOF = 3
digits = set(list("0123456789"))
lettersdigitsunderscore = set(list("abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ_0123456789"))
letters = set(list("abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"))
ws = set(list(" \t\n\r"))
badidentifiertoken = 1
notAChar = 2

class StreamReader:

    def __init__(self, instream):
        self.instream = instream
        self.nextChars = ""
        self.EOF = False
        self.line = 1
        self.column = 0
        self.charsRead = 0


    def readChar(self):

        if len(self.nextChars) > 0:
            nextChar = self.nextChars[0]
            self.nextChars = self.nextChars[1:]

        else:
            nextChar = self.instream.read(1)

        if nextChar == "":
            nextChar = chr(EOF)

        elif nextChar == '\n':
            self.line+=1
            self.column = 0

        else:
            self.column+=1


        if nextChar == chr(EOF):
            self.EOF = True

        self.charsRead += 1

        return nextChar

    def unreadChar(self, ch):
        if len(ch) == 0:
            return

        if len(ch) != 1:
            raise Exception(notAChar)

        self.EOF = False

        self.nextChars = ch + self.nextChars

        if ch == '\n':
            self.line-=1
        else:
            self.column-=1

        self.charsRead -= 1

    def numCharsRead(self):
        # return the number of characters read. This is useful when backtracking is performed
        # in case no progress is being made in reading the stream.
        return self.charsRead

    def eof(self):
        return self.EOF

    def readUpTo(self, delimiter):
        result = ""

        done = False

        while not done and not self.eof():

            c = self.readChar()

            if not self.eof():
                result += c

            if result[-len(delimiter):] == delimiter:
                done = True

        return result

    def readInt(self):
        number = ""

        self.skipWhiteSpace()

        digit = self.readChar()

        while digit in digits:
            number += digit
            digit = self.readChar()

        self.unreadChar(digit)

        return int(number)

    def readIdentifier(self):
        id = ""

        self.skipWhiteSpace()

        c = self.readChar()

        if not c in letters:
            print("Bad identifier token found in source file starting with", c, "at line", self.line, "and column", self.column)
            raise Exception(badidentifiertoken)

        while c in lettersdigitsunderscore:
            id += c
            c = self.readChar()

        self.unreadChar(c)

        return id

    def skipWhiteSpace(self):
        c = self.readChar()

        while c in ws:
            c = self.readChar()

        self.unreadChar(c)


    def peek(self, value):
        # Skip white space, then look for the value as the next characters in the input file.
        # Remember the read characters, but return true if they are found and false otherwise.

        readChars = ""

        self.skipWhiteSpace()

        done = False

        while len(readChars) < len(value) and not done:
            c = self.readChar()
            if c == EOF:
                done = True
            else:
                readChars += c

        for i in range(len(readChars)-1,-1,-1):
            self.unreadChar(readChars[i])

        if readChars == value:
            return True

        return False

    def skipComments(self):
        # skip comments

        while self.peek("(*"):
            self.readUpTo("*)")

    def getLineNumber(self):
        return self.line

    def getColNumber(self):
        return self.column

    def getToken(self):
        self.skipWhiteSpace()
        c = self.readChar()

        if c in digits:
            self.unreadChar(c)
            return self.readInt()

        if c in letters:
            self.unreadChar(c)
            return self.readIdentifier()

        return c

Fig. 2.3: The StreamReader Class - streamreader.py

2.5. An NFA Example

This section presents an an NFA (a non-deterministic finite statement machine) implementation as an example only. Because of its non-deterministic nature, it uses backtracking search to determine if a string is accepted by the machine or not. NOTE that null transitions are denoted as epsilon and not lambda.

To implement this example, the NFA state must be defined because the transition function of a non-deterministic machine takes a state and an input symbol and returns a set of states.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class NFAState:
    def __init__(self, id, acceptsTokenId = None, transitions = {}):
        # An id of -1 is not allowed since that indicates there is
        # no transition on a value.
        if id == -1:
            raise Exception("A state id of -1 is not allowed.")

        self.id = id
        # A copy of the list of transitions needs to be created
        # because Python makes only one instance of a default
        # parameter. Changing the list later, by adding a transition
        # would add that transition to every state. Wow! Talk about
        # bad semantics...
        self.transitions = dict(transitions)

        self.acceptsTokenId = acceptsTokenId

        # This will cause onGoTo to generate an Exception if called
        # before the setClasses method is called.
        self.classes = None

    def setClasses(self, classes):
        self.classes = classes

    def addTransition(self, onClass, toStateId):
        if onClass in self.transitions:
            self.transitions[onClass].add(toStateId)
        else:
            self.transitions[onClass] = set([toStateId])

    def hasTransition(self, onClass):
        return onClass in self.transitions

    def onClassGoTo(self, onClass):
        if onClass in self.transitions:
            return self.transitions[onClass]

        return set([])

    # You must call setClasses before calling the onGoTo method.
    def onGoTo(self, on):
        for aClass in self.transitions:
            if on in self.classes[aClass]:
                return self.transitions[aClass]

        return set([])

    def getTransitions(self):
        return self.transitions

    def getId(self):
        return self.id

    def setAccepting(self, tokenId):
        self.acceptsTokenId = tokenId

    def isAccepting(self):
        return self.acceptsTokenId != None

    def getAcceptsTokenId(self):
        return self.acceptsTokenId

    def __repr__(self):
        return "NFAState(" + repr(self.id) + "," + repr(self.acceptsTokenId) + "," + \
            repr(self.transitions) + ")"

    def __str__(self):
        val = ""
        val = "NFAState " + str(self.id) + "\n"
        if self.acceptsTokenId != None:
            val += "    accepts token with identifier: " + str(self.acceptsTokenId) + "\n"

        for onClass in self.transitions:
            for toStateId in self.transitions[onClass]:
                val += "    On " + str(on) + " Go To " + str(toStateId) + "\n"

        return val

Fig. 2.4: The NFA State Class

The code in figure 2.5 completes the NFA example code. It employs recursive backtracking through the acceptsSuffix function. Notice that when onGoTo and onClassGoTo are called that a set of state ids is returned, even if there is only one state in the set.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
import nfastate
import io
import streamreader

# This NFAStateMachine demonstrates backtracking search while trying
# to find a means of accepting a string of characters. The NFA allows
# the use of "epsilon" transitions and cycles of "epsilon" transitions.
# It avoids getting stuck in a cycle by keeping track of visited
# "states". The state of the NFA is determined not only by the nfa
# state it is in, but also by the state of the stream it is reading.
# A cycle occurs when a state is visited twice with the same number
# of characters read from the stream.

class NFAStateMachine:
    def __init__(self, states, startStateId, classes):
        self.states = states
        self.startStateId = startStateId
        self.classes = classes

        for stateId in self.states:
            self.states[stateId].setClasses(classes)

    def accepts(self, strm):
        # The accepts method uses a recursive acceptsSuffix
        # which starts in the given state (not necessarily the
        # start state) and recursively uses search with backtracking
        # to try to find a final state with all of the input consumed.
        # If it is successful on this path then it returns True and if
        # not it returns False to continue to backtrack and look for
        # another path to a final state.

        def acceptsSuffix(stateId):
            #print("trying", stateId, "with", strm.numCharsRead(), "characters read")

            # If we are not making any progress, we must backtrack.
            if (stateId, strm.numCharsRead()) in visited:
                #print("backtracking from", stateId, "already visited")
                return False

            # Otherwise, add the (stateId, number of characters read) to the
            # set of visited states.
            visited.add((stateId, strm.numCharsRead()))
            theState = self.states[stateId]


            # Check that we are not at end of file and in an accepting state.
            c = strm.readChar()
            if strm.eof() and theState.isAccepting():
                #print(stateId)
                return True

            strm.unreadChar(c)

            for onClass in theState.getTransitions():
                toStateIds = theState.getTransitions()[onClass]

                if onClass == "epsilon":
                    for toStateId in toStateIds:
                        if acceptsSuffix(toStateId):
                            #print(stateId)
                            return True

                else: # onClass is not an epsilon transition
                    c = strm.readChar()

                    for toStateId in toStateIds:
                        if c in self.classes[onClass] and acceptsSuffix(toStateId):
                            #print(stateId)
                            return True

                    strm.unreadChar(c)

            #print("backtracking from", stateId)
            return False

        # This set will take care of keeping track of all traversed
        # states and characters read from the stream. If progress is
        # not made, then we must backtrack.
        visited = set()

        # Beginning of accepts function body - We call acceptsSuffix
        # initially starting from the start state.
        return acceptsSuffix(self.startStateId)


def main():

    q0 = nfastate.NFAState(0)
    q1 = nfastate.NFAState(1,1)
    q2 = nfastate.NFAState(2)
    classes = {"zero":frozenset(["0"]), "one":frozenset(["1"]), "epsilon":frozenset([])}

    q0.addTransition("zero", 1)
    q0.addTransition("one", 1)
    q1.addTransition("zero", 0)
    q1.addTransition("one",1)
    q1.addTransition("zero",2)
    q2.addTransition("epsilon", 0)
    q0.addTransition("epsilon", 2)
    q2.addTransition("one",1)

    nfa = NFAStateMachine({0:q0, 1:q1, 2:q2}, 0, classes)

    done = False

    s = input("Please enter a string of zeros and ones (type done to quit): ").strip()

    while s!="done":

        strm = streamreader.StreamReader(io.StringIO(s))

        if nfa.accepts(strm):
            print("The string is accepted by the finite state machine.")
        else:
            print("The string is not accepted.")

        s = input("Please enter a string of zeros and ones (type done to quit): ").strip()

    print("Program Completed.")

if __name__=="__main__":
    main()

Fig. 2.5: An NFA Example

2.6. A Scangen Input File

Here is a Scangen input file for the JPython programming language.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
(* This a sample input file for the scangen.py program. The
   program reads an input file like this one and produces a
   scanner which is capable of tokenizing the input for the
   programming language defined in this file. For instance,
   this file defines the programming language for a variant
   of Python I have called JPython. It is a combination of
   Java and Python.

   Here is a sample program from that language.

        # In JPython you can declare functions and variables.
        # Functions are declared/defined with a def keyword.
        def factorial(n) {
                if (n == 0)
                        return 1;

                # This involves a recursive call. Statements are
                # terminated with semicolons.
                return n * factorial(n-1);
        }


        def iterativeFactorial(n) {
                # The decl is to declare a local variable.
                decl result = 1;
                for i in range(1,n+1) {
                        result = result * i;
                }

                return result;
        }



        def main() {
                print("The factorial of 5 is", factorial(5));
                print('The iterative factorial of 5 is', iterativeFactorial(5));
        }

*)

(* Comments for the scangen input file appear
   within paren asterisk pairs as shown here. *)

#CLASSES


(* The classes defines classes of ASCII character codes. All
   supported variants of the class definitions are shown here.
   The ^ operator means that the class includes all ASCII
   codes (i.e. 0 to 255) that are NOT the given character
   codes. The names of the classes below describe their
   true nature.
*)

anycharbutnewline = ^10..13;
anycharbutquote = ^39;
anycharbutdoublequote = ^'"';
quote = 39;
doublequote = '"';
pound = '#';
letter  = 'A'..'Z', 'a'..'z';
digit   = '0'..'9';
EOF     = 3;

#KEYWORDS

(* Keywords are optional but define the identifier tokens that should
   be recognized as keywords and not identifiers.

   The number is a token identifier that may be used instead of the actual
   string to identify the keyword. Constants like the name def_keyword
   are defined by scangen for each keyword identifier in the generated scanner.

   Tokens print, range, True, False are all bindings that exist during code
   generation so are not recognized as keywords.
*)

'def';
'if';
'while';
'len';
'and';
'not';
'or';
'return';
'in';
'None';
'for';
'else';
'decl';
'True';
'False';


#TOKENS

(* The identifier token must be the first token defined in this list for the keyword
   definitions given above.

   The token identifier numbers also have constants defined for them like the name
   identifier_token for instance. These names are created by the scangen program in the
   generated scanner.

   The name "comment" is a special name. If used, it represents comments that are to be
   ignored by the scanner. Comment tokens are filtered out by the generated scanner.

*)


identifier = letter.(letter|digit)*;
integer = digit.digit*;
'>=';
'<=';
'==';
'!=';
'>';
'<';
'=';
'(';
')';
'+';
'-';
'*';
'/';
'[';
']';
'{';
'}';
',';
';';
stringconst = (quote . anycharbutquote* . quote) | (doublequote . anycharbutdoublequote* . doublequote);
comment = pound . anycharbutnewline*;
endoffile = EOF;

#DEFINITIONS

from jpythonbackend import *

#PRODUCTIONS

Program ::= Block endoffile                                             (JBlock(Block));

Block ::= FunDecs VarDecs Statements                                    ((FunDecs,VarDecs,Statements));

FunDecs ::= null                                                        ([]);
          | 'def' identifier '(' ArgList ')' CompoundStmt FunDecs       ([JFundec(identifier, ArgList,CompoundStatement)]+FunDecs);

VarDecs ::= null                                                        ([]);
          | 'decl' identifier ';' VarDecs                               ([JDecl(identifier)]+VarDecs);

Statements ::= null                                                     ([]);
             | TerminatedStatement Statements                           ([TerminatedStatement]+Statements);

TerminatedStatement ::= Statement ';'                                   (Statement);

CompoundStmt ::= '{' Block '}'                                          (JBlock(Block));

Statement ::= AssignmentStmt                                            (AssignmentStmt);
            | ReturnStmt                                                (ReturnStmt);
            | IfStmt                                                    (IfStmt);
            | WhileStmt                                                 (WhileStmt);
            | ForStmt                                                   (ForStmt);
            | CompoundStmt                                              (CompoundStmt);

AssignmentStmt ::= identifier '=' Expression                            (JAssign(identifier,Expression));

ReturnStmt ::= 'return' OptionalExpression                              (JReturn(OptionalExpression));

OptionalExpression ::= null                                             (None);
                     | Expression                                       (Expression);

IfStmt ::= 'if' '(' Expression ')' Statement OptionalElse               (If(Expression,Statement,OptionalElse));

OptionalElse ::= null                                                   (Pass);
               | 'else' Statement                                       (Statement);

WhileStmt ::= 'while' '(' Expression ')' Statement                      (While(Expression,Statement));

ForStmt ::= 'for' identifier 'in' Expression Statement                  (For(identifier,Expression,Statement));

Expression ::= Expression 'or' AndExpression                            (OrExpr(Expression,AndExpression));
             | AndExpression                                            (AndExpression);

AndExpression ::= AndExpression 'and' NotExpression                     (AndExpr(AndExpression,NotExpression));
                | NotExpression                                         (NotExpression);

NotExpression ::= 'not' RelExpression                                   (NotExpr(RelExpression));
                | RelExpression                                         (RelExpression);

RelExpression ::= NumExpression RelOp NumExpression                     (relexpr(RelOp,NumExpression1,NumExpression2));
                | NumExpression                                         (NumExpression);

RelOp ::= '>='                                                          ('>=');
        | '<='                                                          ('<=');
        | '>'                                                           ('>');
        | '<'                                                           ('<');
        | '=='                                                          ('==');
        | '!='                                                          ('!=');

NumExpression ::= NumExpression '+' Term                                (AddExpr(NumExpression,Term));
                | NumExpression '-' Term                                (SubExpr(NumExpression,Term));
                | Term                                                  (Term);

Term ::= Term '*' Factor                                                (mulexpr(Term,Factor));
       | Term '/' Factor                                                (divexpr(Term,Factor));
       | Factor                                                         (Factor);

Factor ::= identifier                                                   (identexpr(identifier));
         | integer                                                      (intexpr(integer));
         | FunCall                                                      (FunCall);
         | '(' ExpressionList ')'                                       (tuple(ExpressionList));
         | 'True'                                                       (boolexpr(True));
         | 'False'                                                      (boolexpr(False));
         | stringconst                                                  (strexpr(stringconst));

FunCall ::= identifier '(' ArgList ')'                                  (funcall(identifier,ArgList));

ArgList ::= null                                                        ([]);
          | ExpressionList                                              (ExpressionList);

ExpressionList ::= Expression                                           ([Expression]);
                 | Expression comma ExpressionList                      ([Expression]+ExpressionList);

IdentList ::= identifier                                                ([identifier]);
            | identifier ',' IdentList                                  ([identifier]+IdentList);

#END

Fig. 2.6: A Scangen Input File - jpython.txt

2.7. NFA to DFA Conversion

This is slight variation of the algorithm presented on page 59 of Linz, 5th edition.

2.7.1. The 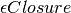\epsilon Closure Function

In this version of the algorithm we define a function called 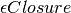\epsilon Closure that given a set of states of an NFA returns the set of states that can be reached on epsilon transitions from the given set of states.

The closure set can be computed by starting with a stack of the given set of states. Then the stack is repeatedly popped until it is empty. Each time a state is popped any states that can be reached from the popped state on an \epsilon transition, and that are not yet in the closure set, are pushed onto the stack and added to the closure set. Once the stack is emptied there are no more \epsilon reachable states from the original given set of states and the \epsilon-closed set is returned.

2.7.2. The NFA to DFA Algorithm

For 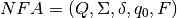NFA = (Q,\Sigma,\delta,q_0,F) we can form a DFA by starting with 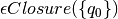\epsilon Closure(\{q_0\}) as the start state of the DFA. We may wish to simply make a mapping from a DFA state id to the set of NFA states it represents and another mapping from NFA state sets to the DFA state it represents. For the mapping from NFA state sets to DFA states you will need to use frozenset in Python because only immutable values may be used as keys in a dictionary. We put this DFA state on a stack of unexplored states.

To complete the DFA we do the following:

  1. We pop a DFA state from the stack of unexplored states.
  2. We form a new set of NFA states as described in step 2 of the algorithm on page 59 of Linz. Remember to form the \epsilon Closure of the new states. If the newly formed set of NFA states already exists in the DFA we form a transition from the current state to the DFA state corresponding to the set of NFA states we just found.
  3. If the newly formed state (i.e. set of NFA states) does not exist in the DFA then we add a new state to the DFA and form a transition from the current state to the newly formed state. We also add the new state to the stack of unexplored states.

When we have emptied the stack we have formed the DFA. The start state of the DFA contains the start state of the NFA. Accepting states of the DFA contain an accepting state of the original NFA.

2.7.3. Example Calculator Language

Consider a calculator language that has the ability to store and recall from a memory location. It can also get input from the keyboard, it has the ability to add, subtract, multiply, and divide. Finally it can raise a number to an exponent. The tokens of this language might be parens, s for store, r for recall, i for reading an input value, numeric operators (i.e. +,-,*,/), numbers, and the carat (i.e. ^) for raising a value to an exponent. An NFA to recognize these tokens is provided here. A description of the NFA for this calculator language is provided here.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
The start state is: 0

STATE     ON CLASS     GO TO     ACCEPTS
-----     --------     -----     -------
    0
           EPSILON        31
           EPSILON        33
           EPSILON        35
           EPSILON        37
           EPSILON        39
           EPSILON        41
           EPSILON        43
           EPSILON        45
           EPSILON        47
           EPSILON        49
           EPSILON        51

    1
             digit         2

    2
           EPSILON         5

    3
             digit         4

    4
           EPSILON         6

    5
           EPSILON         3
           EPSILON         6

    6
           EPSILON         5
           EPSILON         8

    7
           EPSILON         1

    8
           EPSILON        19

    9
            period        10

   10
           EPSILON        11

   11
             digit        12

   12
           EPSILON        14

   13
           EPSILON         9

   14
           EPSILON        17

   15
             digit        16

   16
           EPSILON        18

   17
           EPSILON        15
           EPSILON        18

   18
           EPSILON        17
           EPSILON        20

   19
           EPSILON        13

   20
           EPSILON        22

   21
           EPSILON         7

   22
           EPSILON        32

   23
             digit        24

   24
           EPSILON        27

   25
             digit        26

   26
           EPSILON        28

   27
           EPSILON        25
           EPSILON        28

   28
           EPSILON        27
           EPSILON        30

   29
           EPSILON        23

   30
           EPSILON        32

   31
           EPSILON        21
           EPSILON        29

   32                               yes

   33
                 s        34

   34                               yes

   35
                 r        36

   36                               yes

   37
                 i        38

   38                               yes

   39
                 (        40

   40                                yes

   41
                 )        42

   42                                yes

   43
                 +        44

   44                                yes

   45
                 *        46

   46                                yes

   47
                 /        48

   48                                yes

   49
                 -        50

   50                                yes

   51
                 ^        52

   52                                yes

The DFA that results from converting this NFA to a DFA using the algorithm presented in this section looks like this. This assumes that accepting states that accept different values cannot be merged into one accepting state but must remain separate.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
The start state is: 0

STATE     ON CLASS     GO TO     ACCEPTS
-----     --------     -----     -------
    0
                 (         1
                 )         2
                 *         3
                 +         4
                 -         5
                 /         6
                 ^         7
             digit         8
                 i         9
                 r        10
                 s        11

    1                             yes

    2                             yes

    3                             yes

    4                             yes

    5                             yes

    6                             yes

    7                             yes

    8                             yes
             digit        12
            period        13

    9                             yes

   10                             yes

   11                             yes

   12                             yes
             digit        12
            period        13

   13
             digit        14

   14                             yes
             digit        15

   15                             yes
             digit        15

2.8. DFA Minimization

It is possible to minimize the number of states required for a DFA. The minimization algorithm proceeds by making two initial states: one containing all non-final states and one containing all final states. We’ll call these two initial state sets partitions. A procedure called finer is called repeatedly on each partition to split the partitions into progressively smaller and smaller partitions until no more partitions are created.

2.8.1. The Finer Function

Finer is given a partition identifier, identifying one partition of the original set of states. Finer proceeds by looking at each transition for all states within the partition. One dfa state is picked from the partition as the primary state. If a transition is found on a class of characters that goes to a partition that differs from the primary state’s partition on the same transition class, the two states are distinguishable and the secondary state is added to a set of distinquished states.

After going through all the alphabet symbols (i.e. classes of characters) in the partition, if the set of distinquished states is not empty then all the newly discovered distinquished states are added to a new partition and removed from the current partition. If a new partition was created, finer returns true. Otherwise it returns false.

2.8.2. Example Minimal DFA

The example DFA from the previous section is defined by the Python code found here. The minimized DFA for the DFA presented in the previous section is given below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
The start state is: 0

STATE     ON CLASS     GO TO     ACCEPTS
-----     --------     -----     -------
    0
                 (         1
                 )         1
                 *         1
                 +         1
                 -         1
                 /         1
                 ^         1
             digit         3
                 i         1
                 r         1
                 s         1

    1                             yes

    2
             digit         4

    3                             yes
             digit         3
            period         2

    4                             yes
             digit         4

Finer finds that it needs to split when considering the transitions in this order (for example):

  • found a difference on ( from state 0
  • found a difference on ) from state 0
  • found a difference on * from state 0
  • found a difference on + from state 0
  • found a difference on - from state 0
  • found a difference on / from state 0
  • found a difference on ^ from state 0
  • found a difference on i from state 0
  • found a difference on r from state 0
  • found a difference on s from state 0
  • found a difference on digit from state 1
  • found a difference on period from state 1
  • found a difference on digit from state 1
  • found a difference on period from state 1
  • found a difference on digit from state 1
  • found a difference on digit from state 1
  • found a difference on period from state 3
  • found a difference on period from state 3

While the ordering of splits might be random, the minimal DFA generated is not random. The same resulting minimized DFA will always result from the minimization algorithm.

2.9. Regular Expressions To NFAs

An NFA can be built from a regular expression as described in the text. This is a description of how to take an input file describing tokens of a programming language by regular expressions and turn it into a NFA for recognizing those tokens. Consider the following description of a programming language.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
(* Comments for the scangen input file appear
   within paren asterisk pairs as shown here. *)

#CLASSES


(* The classes defines classes of ASCII character codes. All
   supported variants of the class definitions are shown here.
   The ^ operator means that the class includes all ASCII
   codes (i.e. 0 to 255) that are NOT the given character
   codes. The names of the classes below describe their
   true nature.
*)

anycharbutnewline = ^10..13;
anycharbutquote = ^39;
anycharbutdoublequote = ^'"';
quote = 39;
doublequote = '"';
pound = '#';
letter  = 'A'..'Z', 'a'..'z';
digit   = '0'..'9';
EOF     = 3;

#KEYWORDS

(* Keywords are optional but define the identifier tokens that should
   be recognized as keywords and not identifiers.

   The number is a token identifier that may be used instead of the actual
   string to identify the keyword. Constants like the name def_keyword
   are defined by scangen for each keyword identifier in the generated scanner.

   Tokens print, range, True, False are all bindings that exist during code
   generation so are not recognized as keywords.
*)

'def';
'if';
'while';
'len';
'and';
'not';
'or';
'return';
'in';
'None';
'for';
'else';
'decl';
'True';
'False';


#TOKENS

(* The identifier token must be the first token defined in this list for the keyword
   definitions given above.

   The token identifier numbers also have constants defined for them like the name
   identifier_token for instance. These names are created by the scangen program in the
   generated scanner.

   The name "comment" is a special name. If used, it represents comments that are to be
   ignored by the scanner. Comment tokens are filtered out by the generated scanner.

*)


identifier = letter.(letter|digit)*;
integer = digit.digit*;
'>=';
'<=';
'==';
'!=';
'>';
'<';
'=';
'(';
')';
'+';
'-';
'*';
'/';
'[';
']';
'{';
'}';
',';
';';
stringconst = (quote . anycharbutquote* . quote) | (doublequote . anycharbutdoublequote* . doublequote);
comment = pound . anycharbutnewline*;
endoffile = EOF;

The tokens for this language are described by regular expressions in the #Tokens section of the input file. These regular expressions either start with a token name, like identifier or they are given as a string of characters. Either way, these regular expressions may be converted into NFA’s by the execution of an infix evaluator for regular expressions. The algorithm is presented below.

2.9.1. The Algorithm

The algorithm uses two stacks, an operator stack and an operand stack. The operator stack will hold operators and left parens. The operand stack holds NFAs which are composed of a tuples of states consisting of a start and stop state for each NFA.

The algorithm proceeds by scanning the infix expression as a string from left to right getting the tokens from the string. The tokens represent classes of characters and operators (including parens).

Each operator has a precedence associated with it. The Kleene Star has the highest precedence while follows (i.e. the period or juxtaposition) has the next lower precedence followed by choice (i.e. the + or the |) with the next lower precedence. Finally the left paren and right paren precedence are the lowest in precedence.

To begin the operandStack and the operatorStack are created and a left paren is pushed on the operator stack.

We read a regular expression from the input file given above. We will call each input symbol of the regular expression a token. If the token is not a semicolon we perform the following steps:

  • If the token is an operator then we need to operate on the two stacks with the given operator.
  • If the token is a character class then we form an NFA with two states and push the NFA’s start and stop states on the operand stack as a tuple.

After scanning all the input and operating when required we operate on the stacks one more time with the two stacks and a right paren operator. At this point the operator stack should be empty and the operand stack should have one number on it which is the result. You pop the operand stack to get the NFA for that regular expression.

2.9.2. The Operate Function

My suggestion is to write this as a separate function in your program. The operate function is passed an operator and the operator stack and operand stack as arguments. To operate we do the following. If the given operator is a left paren we push it on the operator stack and return. Otherwise, while the precedence of the given operator is less than or equal to the precedence of the top operator on the operator stack we do the following:
  1. Pop the top operator from the operator stack. Call this the topOp.
  2. If the topOp is a Kleene Star, choice, or follows operator then operate on the operand stack by popping the operands, forming a new NFA with possible epsilon transitions, and pushing the resulting NFA’s starting and ending states as a tuple.
  3. If the topOp is a left paren then the given operator should be a right paren. If so, we are done operating so simply return from the operate procedure at that point discarding the right paren.

When the precedence of the operator is greater than the precedence of the topOp the loop terminates and we push the given operator on the operator stack before returning from operating.

This finishes the operate function and the infix evaluator. Each NFA is built by the program and one new state with epsilon transitions to each of the starting states of the regular expressions is constructed to build one NFA for all the regular expressions specified in the input file.

2.9.3. Reading the Input

Reading the regular expression input can be accomplished using the StreamReader class. Because reading the input can be a little daunting at first, a shell program called RE2NFA.py is provided to aid you in reading the input. You still must write a little of the code to read the regular expressions themselves, but you have plenty of sample code to look at in the shell program to see how to use the StreamReader object called reader in the code.

2.10. Programming Exercises

Here are a few programming exercises that go along with chapter 2 of the text.

  1. Build a DFA for the finite state machine presented in figure 2.7 of the text. You should implement a class called FiniteStateMachine that takes a dictionary of states as input to its constructor along with an integer indicating its start state. For example, the code below would create a Finite State Machine for the DFA in figure 2.1 of the text.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
    import state
import io
import streamreader

class FiniteStateMachine:
    def __init__(self, states, startStateId, classes):
        self.states = states
        self.startStateId = startStateId
        self.classes = classes

        for stateId in self.states:
            self.states[stateId].setClasses(classes)

    def accepts(self, strm):
        pass # You must complete this function

def main():

    q0 = state.State(0)
    q1 = state.State(1,1)
    q2 = state.State(2)
    classes = {"zero":frozenset("0"), "one":frozenset("1")}

    q0.addTransition("zero", 0)
    q0.addTransition("one", 1)
    q1.addTransition("zero", 0)
    q1.addTransition("one",2)
    q2.addTransition("zero",2)
    q2.addTransition("one",1)

    dfa = FiniteStateMachine({0:q0, 1:q1, 2:q2}, 0, classes)

    # You must complete the main function here but you can
    # create a stream over a string s by writing
    # strm = streamreader.StreamReader(io.StringIO(s))

if __name__=="__main__":
    main()

    Then, there should be a method called accepts that takes a stream as input and returns true or false if the string is accepted by the finite state machine.

    The stream can be created by reading a string from the user and building a StringIO object over it and then a StreamReader object over the StringIO object. The program should read the string from the user by prompting the user to enter it, then it should print that the string was accepted or not. The program should continue to read strings, one line at a time, until an empty line is printed.

    You should use the state class from section 2.1 for your DFA states. The tokenId that may be passed on the constructor can be the state identifier for accepting states of your DFA.

    When run, the interaction should look like this. Your output must match this sample output exactly to be considered correctly solved.

    1
2
3
4
5
6
7
8
    Please enter a string of a's and b's: aaabbabbaaaaabbabbbbaa
That string is accepted by this finite state machine.
Please enter a string of a's and b's: abcdefg
That string is not accepted.
Please enter a string of a's and b's: abbababababab
That string is not accepted.
Please enter a string of a's and b's:
Program Completed.

  2. Build a DFA as described in problem one for the sets of strings described in the text in exercise 2 (a)-(e) of the text on page 47.

  3. Build a DFA as described in problem one for the sets of strings described in the text in exercise 7 (a)-(g) of the text on page 47.

  4. Build a DFA as described in problem one for the sets of strings described in the text in exercise 8 (a)-(d) of the text on page 47.

  5. Build an NFA as described in problem 14 on page 48 with epsilon transitions. Then run the NFA to DFA algorithm on it to produce a DFA. For example, consider the following NFA.

      1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
    import sys
import stack
import state
import nfastate
import streamreader
import orderedcollections

epsilon = "epsilon"

class NFA:
    def __init__(self,classes,states):
        self.states = states
        self.classes = classes

class DFA:
    def __init__(self, classes=orderedcollections.OrderedMap(), states=orderedcollections.OrderedMap()):
        self.classes = orderedcollections.OrderedMap(classes)
        self.states = orderedcollections.OrderedMap(states)
        self.numStates = len(states)


    def __repr__(self):
        return ("DFA(" + repr(self.classes) + "," + repr(self.states) + ")")


    def buildFromNFA(self,nfa):
        def newState():
            # Add a new state to the map of stateIds to states in the state map.
            # Return the new state id.
            pass

        def getAcceptingTokenId(stateSet):
            # Return the first accepting tokenId found in the NFA state set. Otherwise, return None
            pass

        def EPSclosure(stateSet):
            closureSet = orderedcollections.OrderedSet(stateSet)
            # Add to the closure set all NFA state Ids that are
            # in the epsilon closure of this stateSet. Then
            # return the OrderedFrozenSet of this closure set.
            pass


        def nfaTransTo(fromStates, onClass):
            # return the epsilon closure of the set of NFA states that
            # you can get to on the class of characters (i.e. onClass) from
            # this set of fromStates.
            pass


        def gatherClasses(states):
            # return the set of classes of transitions (i.e. classes of characters)
            # that are possible transitions from this set of NFA states.
            pass

        # This is the beginning of the buildFromNFA method.
        # Copy over the classes
        self.classes = nfa.classes


        # Create the start state and the DFA to NFA stateMap.
        self.startStateId = newState()
        self.stateMap = orderedcollections.OrderedMap()


        # Form the epsilon closure of the NFA start state (i.e. state 0) and then
        # map the start state of the DFA to the start state set of the NFA


        # keep track of the new DFA states. The first new DFA state is the start
        # state. You can keep track of this as an ordered set or a stack if you wish.

        # map the set of nfa state ids (as a frozen set) to the new DFA state id in the
        # nfa2dfa map.


        # set the new DFA state to accepting if the NFA states contained an accepting state.
        # You can use the getAcceptingTokenId function for this.


        # While there are no more unexplored states in the new DFA state set, follow the algorithm
        # given on the website by using the nfaTransTo function and creating new DFA states for each
        # new set of NFA states that are found by using gatherClasses. Remember to set accepting states
        # in the DFA as you proceed.

        # Code goes here

    # The writeListing method is provided assuming you used the correct data structures
    # in your code.

    def writeListing(self, outStream):

        outStream.write("The start state is: " + str(self.startStateId) + "\n\n")

        outStream.write("STATE     ON CLASS     GO TO     ACCEPTS\n")
        outStream.write("-----     --------     -----     -------\n")

        for stateId in range(self.numStates):
            if self.states[stateId].isAccepting():
                acceptsId = self.states[stateId].getAcceptsTokenId()
                tokenName = "yes"
            else:
                tokenName = ""

            outStream.write("%5d %34s\n"%(stateId,tokenName))

            trans = self.states[stateId].getTransitions()

            for onClass in trans:
                outStream.write("%18s     %5d\n"%(onClass,trans[onClass]))

            outStream.write("\n")


def main():

    classes = {epsilon:frozenset([]), "zero":frozenset([0]), "one": frozenset([1])}

    q0 = nfastate.NFAState(0)
    q1 = nfastate.NFAState(1,1)
    q2 = nfastate.NFAState(2)


    q0.addTransition("zero", 1)
    q0.addTransition("one", 1)
    q1.addTransition("one", 1)
    q1.addTransition("zero", 0)
    q1.addTransition("zero", 2)
    q1.addTransition(epsilon, 2)
    q2.addTransition("one",1)

    states = {0:q0, 1:q1, 2:q2}

    nfa = NFA(classes, states)

    dfa = DFA()
    dfa.buildFromNFA(nfa)
    dfa.writeListing(sys.stdout)


main()

    Write the required code to get output like the following sample output from running this program. You may assume that state 0 is the start state of the NFA.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
    The start state is: 0

STATE     ON CLASS     GO TO     ACCEPTS
-----     --------     -----     -------
    0
               one         1
              zero         1

    1                                Yes
               one         1
              zero         2

    2
               one         1
              zero         1

  6. Minimize a DFA according to the DFA Minimization algorithm. Use the data provided in the section on DFA minimization. Use the shell program below to get started. You need to complete the three functions that have pass written in them and the calling of finer which is described below and has a comment WRITE THE CODE DESCRIBED ABOVE HERE.

      1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
    # Here is the output from running this.
# Kent's Mac> python3 dfa2mindfa.py
# The MINIMAL DFA CREATED FOR THE REGULAR EXPRESSIONS IS:

# The start state is: 0

# STATE     ON CLASS     GO TO     ACCEPTS
# -----     --------     -----     -------
#     0
#                  a         2

#     1                                yes
#                  a         2

#     2
#                  b         4

#     3
#                  a         1

#     4
#                  b         3

import state
import orderedcollections
import sys


class DFA:
    def __init__(self, classes, states, startStateId):
        self.classes = classes
        self.states = states
        self.startStateId = startStateId

class MinimalDFA:
    def __init__(self):
        self.classes = orderedcollections.OrderedMap()
        self.states = orderedcollections.OrderedMap()
        self.numStates = 0

    def buildFromDFA(self,dfa):
        def newState():
            aState = state.State(self.numStates)
            self.states[self.numStates] = aState
            self.numStates+=1
            return self.numStates-1

        # Returns the Minimized DFA Partition Id given
        # a DFA State and Input symbol class.
        def transToMinPartition(fromDFAStateId, onClass):
            pass

        # Returns an ordered set of all the character classes
        # of all DFA states in a minimized DFA partition.
        def onClasses(minStateId):
            pass

        def finer(minStateId):
            #(********************************************************************************)
            #(* Check each node in the given partition (the one passed as a parameter)       *)
            #(* with the first node in the partition. If a node is found that transitions    *)
            #(* to a different partition than the first node on the same input make a new    *)
            #(* set with this node and put all subsequent nodes that don't have similar      *)
            #(* transitions to the first node into this new set. After going through all     *)
            #(* states, if the new set of distinquished states is not empty then create a    *)
            #(* new partition and then remove all states in the set from the current         *)
            #(* partition and add them to the new partion (i.e. minimal state). Return true  *)
            #(* if a new partition was created and false otherwise. Aho, Sethi, Ullman p. 142*)
            #(********************************************************************************)
            pass


        # Run through all the states and make transitions
        # in the minimized DFA for all transitions that existed
        # in the unminimized DFA. Also sets the state to be accepting
        # if any state in the unminimized DFA was accepting.
        def constructMinStateTransitions():
            for minStateId in self.states:
                minState = self.states[minStateId]

                # Find the first dfa stateid in the set
                dfaStateIds = list(self.min2dfa[minStateId])
                dfaStateIds.sort()
                dfaStateId = dfaStateIds[0]

                if dfa.states[dfaStateId].isAccepting():
                    minState.setAccepting(dfa.states[dfaStateId].getAcceptsTokenId())
                minState.transitions = {}

                trans = dfa.states[dfaStateId].getTransitions()
                for onClass in trans:
                    toDFAStateId = trans[onClass]
                    dfaState = dfa.states[toDFAStateId]
                    toStateId = self.dfa2min[toDFAStateId]
                    minState.addTransition(onClass,toStateId)


            self.startStateId = self.dfa2min[dfa.startStateId]

        self.classes = dfa.classes


        startStateId = newState()
        self.min2dfa = orderedcollections.OrderedMap()
        self.dfa2min = orderedcollections.OrderedMap()

        self.min2dfa[startStateId] = orderedcollections.OrderedSet()

        # Build state sets. One with all
        # the non-final states in it, and one
        # for each accepting state of the dfa
        # since we want separate accepting states
        # for all the tokens of the dfa.

        for stateId in dfa.states:
            dfaState = dfa.states[stateId]

            if not dfaState.isAccepting():
                self.min2dfa[startStateId].add(stateId)
                self.dfa2min[stateId] = startStateId
            else:
                # Now we have to either add another partition (i.e. state) or
                # find the accepting state that this dfa state belongs to.

                found = False

                for minStateId in self.states:
                    minState = self.states[minStateId]
                    if minState.getAcceptsTokenId() == dfaState.getAcceptsTokenId():
                        self.min2dfa[minStateId].add(stateId)
                        self.dfa2min[stateId] = minStateId
                        found = True


                if not found:
                    finalStateId = newState()
                    self.min2dfa[finalStateId] = orderedcollections.OrderedSet([stateId])
                    self.dfa2min[stateId] = finalStateId
                    self.states[finalStateId].setAccepting(dfaState.getAcceptsTokenId())

        self.startStateId = self.dfa2min[dfa.startStateId]

        # Now begin partitioning by finding distinguishable states
        # You must write code here to repeatedly call finer on all states
        # of the minimized DFA until no more changes can be made.

        # WRITE THE CODE DESCRIBED ABOVE HERE.


        # After we are done splitting the states we call constructMinStateTransitions
        # to build the transitions in the new states.
        constructMinStateTransitions()

    def writeListing(self, outStream):

        outStream.write("The MINIMAL DFA CREATED FOR THE REGULAR EXPRESSIONS IS:\n\n")

        outStream.write("The start state is: " + str(self.startStateId) + "\n\n")

        outStream.write("STATE     ON CLASS     GO TO     ACCEPTS\n")
        outStream.write("-----     --------     -----     -------\n")

        for stateId in range(self.numStates):
            if self.states[stateId].isAccepting():
                acceptsId = self.states[stateId].getAcceptsTokenId()
                tokenName = "yes"
            else:
                tokenName = ""

            outStream.write("%5d %34s\n"%(stateId,tokenName))

            trans = self.states[stateId].getTransitions()
            for onClass in trans:
                outStream.write("%18s     %5d\n"%(onClass,trans[onClass]))

            outStream.write("\n")

def main():

    classes = {"a":frozenset(['a']), "b": frozenset(['b'])}

    q0 = state.State(0)
    q1 = state.State(1)
    q2 = state.State(2)
    q3 = state.State(3)
    q4 = state.State(4,1)
    q5 = state.State(5)
    q6 = state.State(6)



    q0.addTransition("a", 1)
    q1.addTransition("b", 2)
    q2.addTransition("b", 3)
    q3.addTransition("a", 4)
    q4.addTransition("a", 5)
    q5.addTransition("b", 6)
    q6.addTransition("b", 3)


    states = {0:q0, 1:q1, 2:q2, 3:q3, 4:q4, 5:q5, 6:q6}

    dfa = DFA(classes, states, 0)

    mindfa = MinimalDFA()
    mindfa.buildFromDFA(dfa)
    mindfa.writeListing(sys.stdout)


main()

7. Write a program that reads a description of a language, like that given in the section on the converting regular expressions to NFA’s in Regular Expressions To NFAs. Use the program shell RE2NFA.py to start your program. Then you must complete the regular expression calculator as described in Regular Expressions To NFAs. See the clearly marked sections of the shell program for what you must complete and what each function should return. Use the file jpython.txt as your input file. The output from your program should then be this nfa.